1-1 振り子の運動方程式
機械式時計の原点は振り子時計にある。歴史的にみても最もシンプルかつ精度の良い機械式時計は振り子式であり、
時計を理論的に解析するためにはまず振り子の運動を解明することが基本となる。
そこでまず手始めに振り子の運動方程式を立ててこれを解いてみよう。
ニュートンの法則から質量$\;m\;$の物体が力$\;F\;$を受けるとき,その物体には力の方向に受けた力に比例した加速度$\;\alpha\;$が生じる。
これは運動している振り子にもそのまま適用される。
式で表せば
\begin{eqnarray}
m\alpha=F
\end{eqnarray}
となる。
振り子の錘には重力の力$\;mg\;$が鉛直下向きに掛かっている。運動方向の力$\;F\;$とは重力の分力である$\;-mgsin\theta\;$のことである。
右方向を$\;\theta\;$が+となるようにとったので - 符号が付いている。
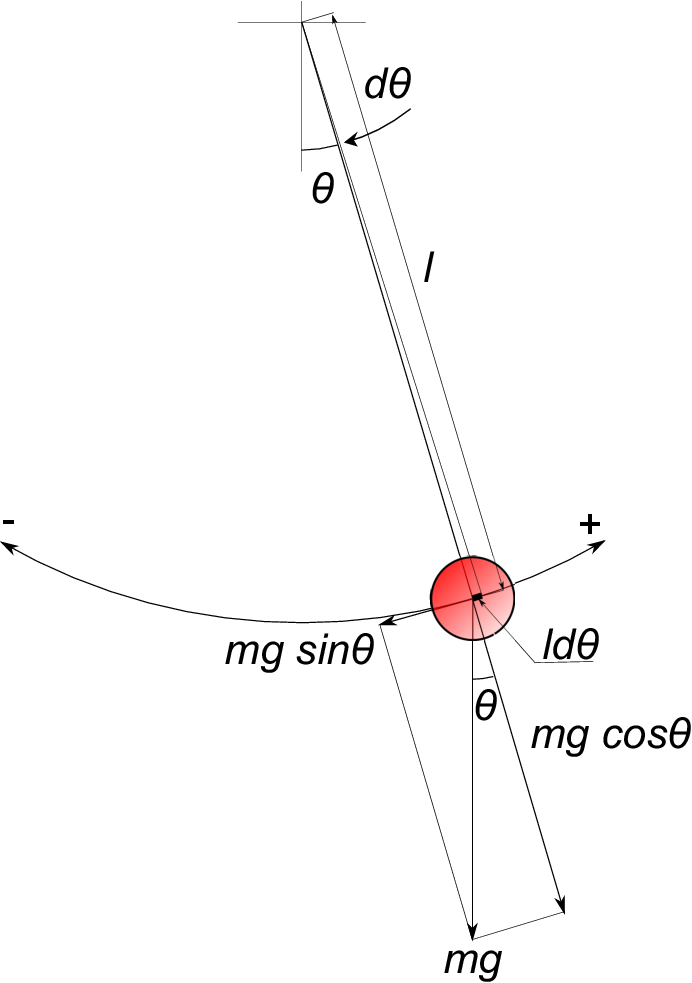
運動方向と直交する$\;mgcosθ\;$は糸の張力と常に釣り合っているのでここでは考えない。
運動方程式を立てるときのコツはまず物体の運動方向に沿って座標軸を決める。
今回の場合は振り子の通る円弧が座標軸であり、$\;\theta\;$が増大する右方向が+である。
次に左辺を$\;m\alpha=\;$とおいて右辺にこの座標軸上(円弧の場合は接線上)のすべての力を書き出す。
今回の場合は$\;-mgsin\theta\;$のみとなる。
この運動方程式を立てるという行為が最も重要なので覚えておくと便利である。
それではまず振り子の速度を求めてみよう。
今振り子が右方向に動いているとして 速度=距離÷時間 だから上図の微小円弧の長さ$\;ld\theta\;$が距離で
これを微小時間$\;dt\;$で割れば(微分すれば)振り子の速度$\;v\;$となる。
\begin{eqnarray}
v=\frac{ld\theta}{dt}
\end{eqnarray}
更に速度$\;v\;$を時間で微分すると加速度$\;\alpha\;$が求められる。
\begin{eqnarray}
α=\frac{dv}{dt}=l\frac{d^2\theta}{dt^2}
\end{eqnarray}
そうすると(1)式より次式が成り立つ。
\begin{eqnarray}
ml\frac{d^2\theta}{dt^2}=-mgsin \theta
\end{eqnarray}
これが自由振動させたときの振り子の運動方程式である。
運動方程式の解き方にはいろいろあるが、本$HP$では振動解析に向いていて比較的簡単に解けるラプラス変換を用いることにする。
ラプラス変換とは$\;t\;$による時間領域を$\;s\;$による複素平面に変換するもので、複素数$\;s\;$の式を変形した後、再度逆ラプラス変換して
$\;t\;$の時間領域に戻すと微分方程式の解が得られるという実に単純な解き方である。
ラプラス変換の証明に関しては多くの数学書に記載があるのでここでは省略するが第5部 数学公式集のラプラス変換表5-3-2の公式を
覚えてしまえば何も考えずに機械的に運動方程式を解くことが出来る。
では早速ラプラス変換を使って(4)式を解いてみよう。
(4)式の両辺を$\;ml\;$で除すと
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l} sin \theta
\end{eqnarray}
ここで$\;\theta\;$が小さいときは
\begin{eqnarray}
sin \theta\approx\theta
\end{eqnarray}
が成り立つ。すなわち
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l} \theta
\end{eqnarray}
となる。
\[\theta_{t=0}=A_0,\;\;\;\;(\frac{d \theta}{d t})_{t=0}=0\]
とおいて両辺をラプラス変換すると(第5部 5-3-2 数学公式集 ラプラス変換表5-3-2参照)
\begin{eqnarray}
&\;&s^2\Theta(s)-s\theta_{t=0}-\left(\frac{d \theta}{dt}\right)_{t=0}=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&s^2\Theta(s)-sA_0=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&(s^2+\frac{g}{l})\Theta(s)=sA_0 \nonumber \\
&\;&\Theta(s)=\frac{sA_0}{(s^2+\frac{g}{l})}
\end{eqnarray}
ラプラス逆変換すると(第5部 数学公式集 ラプラス変換表5-3-2参照)
\begin{eqnarray}
\theta=A_0cos\sqrt{\frac{g}{l}} t
\end{eqnarray}
ここで
\begin{eqnarray}
\omega_n=\pi\;f=\sqrt{\frac{g}{l}}
\end{eqnarray}
を固有振動数と言う。固有振動数とは単位時間当たりの振動の繰り返し回数に1周期の角度$2\pi\;[rad]$を掛けたものであるが
時計の場合は1往復を2回と数えるので$\;\pi f\;$となる。またこれは角速度$\;\omega\;$と混同しないよう注意が必要である。
そうすると式(9)は次のようにあらわすことが出来る。
\begin{eqnarray}
\theta=A_0cos\omega_n t
\end{eqnarray}
周期$T$は
\begin{eqnarray}
T=\frac{2\pi}{\omega_n}={2\pi}\sqrt{\frac{l}{g}}
\end{eqnarray}
式(11)が振り子を自由振動させたときの解であり周期$\;T\;$は振り角$\;A_0\;$に依らず一定となる。
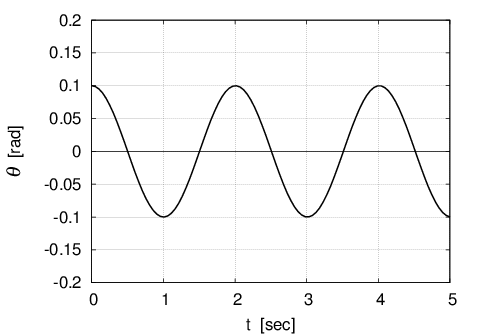
これをグラフで表すと下の図のようになる。
ただし、例として$l=1[m] , g=9.8 [m/s^2] ,A_0=0.1 [rad]$とおいた。
これは上の図で振り子を正の右端に置きそこから手を離した瞬間を時刻0としたとき、その後の時刻における振り子の運動の様子を表している。
この場合の固有振動数$\;\omega_n\;$および周期$\;T\;$は次のようになる。
\begin{eqnarray}
\omega_n&=&\sqrt{\frac{g}{l}}=\sqrt{\frac{9.8}{1}}=3.1305\;[rad/s] \nonumber \\
T&=&\frac{2\pi}{\omega_n}=2\pi\sqrt{\frac{l}{g}}=2\times \pi \times \sqrt{\frac{1}{9.8}}=2.0071\;[sec] \nonumber
\end{eqnarray}