Now, actual motion of pendulum becomes damping motion because of air resistance and some kind of energy scatter at a fulcrum. Such damping is generally referred to as viscous damping and the viscous damping force ''$f_d$'' is represented as shown in the following equation (1) since it is easy to do the mathematical handling. However, as for the true damping mechanism, there have been still a lot of unknown factors in reality.
\begin{eqnarray}
f_d=c\frac{d\theta}{dt}
\end{eqnarray}
Regarding ''$c$'' of the equation (1), it is referred to as viscous damping coefficient.
The pendulum moving on the circular arc receives the resistance force in proportional to the velocity and in the opposite direction of the pendulum movement.
Even if some damping exist at the fulcrum and the thread, all of these factors are regarded as the resistance force ''$f_d$'' to the pendulum.
In other words, if the pendulum is moving in rightward direction, the resistance force ''$f_d$'' works in the same direction as that of the component force of gravity, ''$mg\;sin\theta$'', as shown in the figure below.
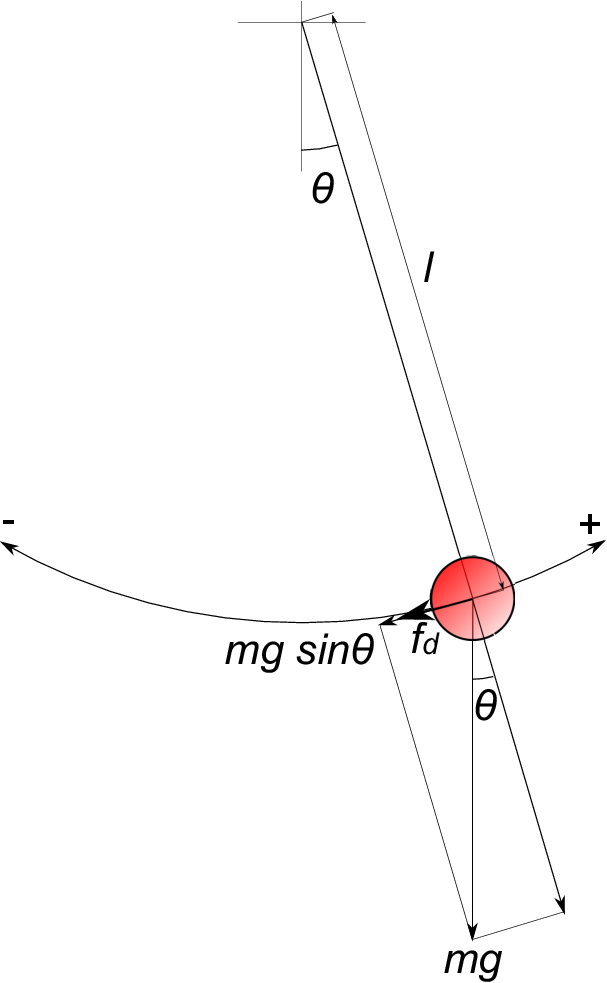
This can be represented in the following equation (2).
\begin{eqnarray}
ml\frac{d^2\theta}{dt^2}&=&-mg\theta-f_d \nonumber \\
&=&-mg\theta-c\frac{d\theta}{dt}
\end{eqnarray}
Dividing the both sides of this equation by ''$ml$'' and transposing the right side to the left side,
the equation (2) can be converted to the equation (3).
\begin{eqnarray}
\frac{d^2\theta}{dt^2}&+\frac{c}{ml}\frac{d\theta}{dt}+\frac{g}{l}\theta=0
\end{eqnarray}
This is the equation of motion of pendulum when the viscous damping needs to be investigated.
Here, ''$\zeta$'' : viscous damping factor, ''$\omega_n$'' : natural frequency and ''$\omega_d$'' : natural frequency of the damping system are defined as equations (4). (5) and (6) respectively.
\begin{eqnarray}
&\zeta&=\frac{c}{2m\sqrt{gl}} \\
&\omega_n&=\sqrt{\frac{g}{l}} \\
&\omega_d&=\sqrt{1-\zeta^2}\;\omega_n
\end{eqnarray}
Then, equation (3) can be converted to the equation (7).
\begin{eqnarray}
\frac{d^2\theta}{dt^2}&+2\zeta\omega_n\frac{d\theta}{dt}+\omega_n^2\theta=0
\end{eqnarray}
Now, let's figure out this equation (7), taking the Laplace transform under the following initial conditions.
\[\theta_{t=0}=A_0 ,\;\;\;\;(\frac{d\theta}{dt})_{t=0}=0\]
As a result of Laplace transform, equation (8) can be obtained.
\begin{eqnarray}
s^2\Theta(s)-s\theta_{t=0}-(\frac{d\theta}{dt})_{t=0}+2\zeta\omega_n(s\Theta(s)-\theta_{t=0})+\omega_n^2\Theta(s)=0\;\;\;\;\;
\end{eqnarray}
This equation (8) can be converted to the equations (9) & (10).
\begin{eqnarray}
s^2\Theta(s)+2\zeta\omega_ns\Theta(s)+\omega_n^2\Theta(s)=A_0(s+2\zeta\omega_n)
\end{eqnarray}
\begin{eqnarray}
(s^2+2\zeta\omega_ns+\omega_n^2)\Theta(s)=A_0(s+2\zeta\omega_n)
\end{eqnarray}
Then, the equation (10) can be converted to the equation (11).
\begin{eqnarray}
\Theta(s)&=&A_0\frac{s+2\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2s} \nonumber \\
&=&A_0\left(\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2s}+\frac{\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2s}\right) \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\} \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+\frac{\zeta\omega_n}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\}
\end{eqnarray}
Then, taking the inverse Laplace transform and using the composition formula of trigonometric function (Section 5 Mathematical Formulas 5-1-9) , the equation (12) can be finally obtained.
\begin{eqnarray}
\theta&=&A_0e^{-\zeta\omega_n t}\{cos\omega_d t+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t\} \nonumber \\
&=&A_0e^{-\zeta\omega_n t}\{cos\omega_d t+\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t\} \nonumber \\
&=&A_0\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
Regarding ''$\phi$'' of the equation (12), it is defined as shown in the equation (13).
\begin{eqnarray}
\phi=tan^{-1}(\frac{\zeta}{\sqrt{1-\zeta^2}})
\end{eqnarray}
This is the solution to the free vibration of the pendulum when the viscous damping needs to be investigated.Making a graph of this equation (12), it becomes the figure below.
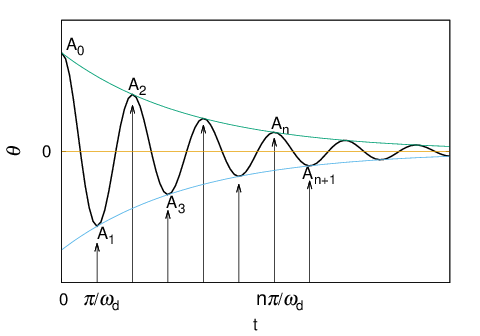
Consequently, damping pendulum represents maximum & minimum values in each ''half oscillation'' which means ''a vibration'' in a terminology of clock /watch.
\begin{eqnarray}
t=\frac{\pi}{\omega_d}
\end{eqnarray}
The equation (15) should be appropriate when the maximum and minimum values are described at this point.
\begin{eqnarray}
\frac{d\theta}{dt}=0
\end{eqnarray}
As ''$\phi$'' is included in the ''$cos$'' form at the right side of the equation (12), a lot of readers may have difficulties in understanding the period of the maximum & minimum values intuitively.
Differentiating the equation (12) with respect to time ''$t$'', the equation (16) can be obtained.
(Refer to Section 5 Mathematical Formulas 5-2-2)
\begin{eqnarray}
\frac{d\theta}{dt}&=&-\frac{A_0}{\sqrt{1-\zeta^2}}\{\zeta\omega_n e^{-\zeta\omega_n t}cos(\omega_d t-\phi)+\omega_d\;e^{-\zeta\omega_n t}sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{A_0}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\omega_n\{\zeta\; cos(\omega_d t-\phi)+\sqrt{1-\zeta^2}\;sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{A_0\;\omega_n}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\;sin\omega_d t
\end{eqnarray}
The equation (16) becomes ''$zero$'' when the ''$t$'' is fulfilled with this condition.
\[t=n\frac{\pi}{\omega_d}\]
Accordingly, ''$\theta$'' is identified to have the maximum or minimum values at this point.
Next, I will actually figure out the maximum & minimum values.
First minimum value, ''$A_1$'' can be obtained by substituting the equation (14) to the equation (12), as shown in the equation (17).
\begin{eqnarray}
|A_1|&=&-|A_0|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos(\pi-\phi) \nonumber \\
&=&|A_0|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos\phi \nonumber \\
&=&|A_0|e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
In the same way, second maximum value, ''$A_2$'' can also be obtained by replacing
''$A_0$'' of the equation (12) with ''$A_1$'', and substituting ''$t$'' ($=\pi/\omega_d$) as shown in the equation (18).
\begin{eqnarray}
|A_2|&=-&|A_1|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos(\pi-\phi) \nonumber \\
&=&|A_1|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos\phi \nonumber \\
&=&|A_1|e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
Then, assuming that numerical differences between ''$|A_0|$'' and ''$|A_2|$'' are ''$\Delta A$'', the equation (19) can be obtained.
\begin{eqnarray}
\Delta A&=&|A_0|-|A_2| \nonumber \\
&=&|A_0|-|A_1|\{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\} \nonumber \\
&=&|A_0|-|A_0|e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\} \nonumber \\
&=&|A_0|(1-e^{-\frac{2\zeta\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&\approx&|A_0|\frac{2\zeta\pi}{\sqrt{1-\zeta^2}}
\end{eqnarray}
This equation shows the result that the exponential power was approximated according to Taylor series expansion. (Refer to Section 5 Mathematical Formulas 5-4)
Similarly, ''$N$'' times of the maximum value,''$A_N$'' is shown as the equation (20).
\begin{eqnarray}
|A_N|=|A_0|e^{-\frac{N\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
''$N+n$'' times of the maximum value,''$A_{N+n}$'' is also shown as the equation (21).
\begin{eqnarray}
|A_{N+n}|=|A_0|e^{-\frac{(N+n)\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
The amplitude loss, ''$\Delta A_n$'' from ''$N$'' times of the maximum value, ''$A_N$'' to the times after ''$n$'' vibration (in a terminology of clock/watch), ''$\Delta A_n$'' can be obtained as shown in the equation (22).
\begin{eqnarray}
\Delta A_n&=&|A_N|-|A_{N+n}| \nonumber \\
&=&|A_0|e^{-\frac{N\zeta\pi}{\sqrt{1-\zeta^2}}} -|A_0|e^{-\frac{(N+n)\zeta\pi}{\sqrt{1-\zeta^2}}} \nonumber \\
&=&|A_0|e^{-\frac{N\zeta\pi}{\sqrt{1-\zeta^2}}} (1-e^{-\frac{n\zeta\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&=&|A_N|(1-e^{-\frac{n\zeta\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&\approx&\frac{n\zeta\pi}{\sqrt{1-\zeta^2}}|A_N|
\end{eqnarray}
Consequently, the amplitude loss in an arbitrary period (2 vibration definition in clock/watch) of the pendulum, ''$\Delta A$'' can be shown as the equation (23).
\begin{eqnarray}
\Delta A&\approx&\frac{2\zeta\pi}{\sqrt{1-\zeta^2}}A \nonumber \\
&=&\frac{c}{2ml}T_d A
\end{eqnarray}
For your note, ''$T_d$'' means the period of pendulum when the damping needs to be investigated,
and defined as the following equation (24).
\begin{eqnarray}
T_d=\frac{2\pi}{\omega_d}
\end{eqnarray}