Cycloid is the trajectory which a certain point on the circular plate plots when that plate is rolled on a certain straight line without sliding. This curve is used for the gear of the watch.
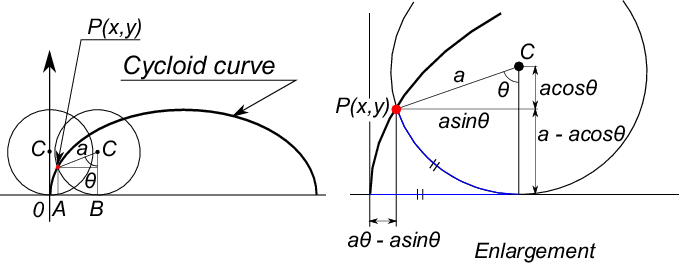
As shown in the figure above, the Cycloid curve becomes the trajectory of the point, ''$P$'' which is fixed on the radius, ''$a$'' when the circle, ''$C$'' whose radius is ''$a$'' is rolled on the ''$x$'' axis without sliding. The coordinates of the respective points can be indicated in the equations of (1) & (2).
\begin{eqnarray}
x&=&a(\theta-sin\theta) \\
y&=&a(1-cos\theta)
\end{eqnarray}
Next, we look at the pendulum which is located between two Cycloid curves as shown in the figure below. Assuming ''$a$'' for radius of the circle, and taking the length of the pendulum thread, ''$4a$'', the trajectory which the pendulum itself plots also becomes Cycloid with offset by $2a$.
The blue curve of the figure below shows the trajectory of the pendulum. This pendulum is called as the Cycloid pendulum.

In case of simple pendulum, the period, ''$T$'' is a function of the displacement, ''$A_0$''.
However, in case of the Cycloidal pendulum, it becomes constant regardless of the displacement.
This can be proven as follows:
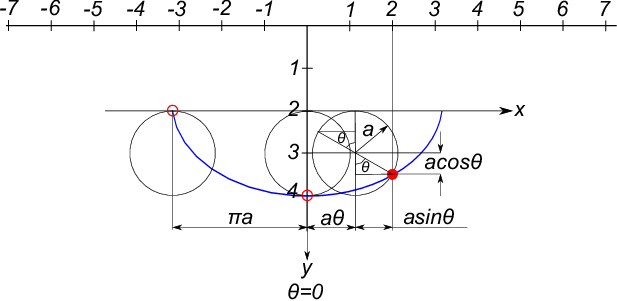
As the figure above shows, the Cycloid trajectory which the pendulum traces can be indicated in the equations (3) & (4).
\begin{eqnarray}
x&=&a\theta+a sin\theta \nonumber \\
&=&a(\theta+sin\theta) \\
y&=&a+acos\theta \nonumber \\
&=&a(1+cos\theta)
\end{eqnarray}
This is equal to what ''$\theta = \pi$'' is transposed with ''$\theta = 0$'' , ''$\theta$'' is measured from the point of
''$\theta= 0$'', and "$y$-axis" is shifted by ''$\pi a$ " in the equations (1) & (2).
Note that ''$\theta$'' is not the displacement of the pendulum here, but the rotation angle of the rolling circle which corresponds to the displacement. Differentiating the equations (3) & (4) with respect to ''$\theta$'', the equations (5) & (6) can be obtained.
\begin{eqnarray}
\frac{dx}{d\theta}&=&a(1+cos\theta) \\
\frac{dy}{d\theta}&=&-asin\theta
\end{eqnarray}
Accordingly, assuming that very little length on the Cycloid curve is ''$ds$'', the equation (7) can be obtained.
\begin{eqnarray}
ds&=&\sqrt{dx^2+dy^2}=\sqrt{a^2(1+cos\theta)^2+a^2sin^2\theta}\;d\theta \nonumber \\
&=&a\sqrt{1+2cos\theta+cos^2\theta+sin^2\theta}\;d\theta \nonumber \\
&=&a\sqrt{2}\sqrt{1+cos\theta}\;d\theta
\end{eqnarray}
The equation (8) can be derived from the law of the conservation of energy, here.
\begin{eqnarray}
\frac{1}{2}mv^2=mg(y-y_0)
\end{eqnarray}
Note that ''$y_0$'' indicates y-axis coordinate of the initial position of the pendulum.
Assuming that ''$\theta_0$'' is the rotation angle of the rolling circle which corresponds to the initial angle of the pendulum, the following equation (9) can be obtained.
\begin{eqnarray}
\frac{1}{2}mv^2&=&mg\{a(1+cos\theta)-a(1+cos\theta_0)\} \nonumber \\
&=&mga(cos\theta-cos\theta_0) \nonumber \\
v&=&\sqrt{2ga(cos\theta-cos\theta_0)}
\end{eqnarray}
In the meantime, as the equation (10) can be indicated, the equation (11) can be obtained.
\begin{eqnarray}
v&=&\frac{ds}{dt}=\frac{a\sqrt{2}\sqrt{1+cos\theta}\;d\theta}{dt} \nonumber \\
&=&\sqrt{2ga(cos\theta-cos\theta_0)}
\end{eqnarray}
\begin{eqnarray}
dt=\sqrt{\frac{a}{g}}\sqrt{\frac{1+cos\theta}{cos\theta-cos\theta_0}}d\theta
\end{eqnarray}
The 1/4 of the period of the pendulum, ''$T/4$'' is what integrated ''$dt$'' from ''0'' to ''$T/4$'', and the rolling angle of the pendulum varies from ''$\theta = 0$'' to ''$\theta = \theta_0$'' during such a range. Accordingly, the equation (12) can be obtained from the equation (11).
\begin{eqnarray}
\int_0^{T/4}dt=\frac{T}{4}=\int_0^{\theta_0}\sqrt{\frac{a}{g}}\sqrt{\frac{1+cos\theta}{cos\theta-cos\theta_0}}d\theta
\end{eqnarray}
Then, the equations (13) & (14) can be indicated from the half-angle formulas of the trigonometric function.
\begin{eqnarray}
cos\frac{\theta}{2}&=&\sqrt{\frac{1+cos\theta}{2}} \\
cos\theta&=&2cos^2\frac{\theta}{2}-1
\end{eqnarray}
Using the equations (13) & (14) with the equation (12), the equation (15) can be obtained.
\begin{eqnarray}
\frac{T}{4}&=&\sqrt{\frac{a}{g}}\int_0^{\theta_0}\frac{cos\frac{\theta}{2}}{\sqrt{cos^2\frac{\theta}{2}-cos^2\frac{\theta_0}{2}}}\;d\theta \nonumber \\
&=&\sqrt{\frac{a}{g}}\int_0^{\theta_0}\frac{cos\frac{\theta}{2}}{\sqrt{sin^2\frac{\theta_0}{2}-sin^2\frac{\theta}{2}}}\;d\theta
\end{eqnarray}
Herewith, implementing such a change of variables, the equation (16) can be derived.
\begin{eqnarray}
u=\frac{sin\frac{\theta}{2}}{sin{\frac{\theta_0}{2}}}
\end{eqnarray}
Differentiating this, the equation (17) can be derived.
\begin{eqnarray}
\frac{du}{d\theta}&=&\frac{cos\frac{\theta}{2}}{2sin{\frac{\theta_0}{2}}} \nonumber \\
d\theta&=&\frac{2sin{\frac{\theta_0}{2}}}{cos\frac{\theta}{2}}du
\end{eqnarray}
Sorting out the equation (15) with the use of the equations (16) & (17), the equation (18) can be obtained
\begin{eqnarray}
\frac{T}{4}&=&2\sqrt{\frac{a}{g}}\int_0^1\frac{du}{\sqrt{1-u^2}}
\end{eqnarray}
Assuming that ''$u = sin \phi$'', the equation (19) can be indicated.
\begin{eqnarray}
\frac{du}{d\phi}=cos\phi \nonumber \\
du=cos\phi \;d\phi
\end{eqnarray}
Accordingly, the equation (20) can be obtained from the equation (18).
\begin{eqnarray}
\frac{T}{4}&=&2\sqrt{\frac{a}{g}}\int_0^{\pi/2}\frac{cos\phi}{cos\phi}\;d\phi \nonumber \\
&=&2\sqrt{\frac{a}{g}}[\phi]_0^{\pi/2} \nonumber \\
&=&\pi \sqrt{\frac{a}{g}}
\end{eqnarray}
The period, ''$T$'' can be converted to the equations (21) & (22) from the equation (20).
\begin{eqnarray}
T&=&2\pi\sqrt{\frac{4a}{g}} \\
&=&2\pi\sqrt{\frac{l}{g}}
\end{eqnarray}
The isochronism of the Cycloidal pendulum is proven here, as shown in the above.
This is called as ''Pendulum of Huygens'', as this was discovered in 17 centuries by Mr.Huygens, Physicist in Netherlands.