次にテンプに更に天真ほぞと軸受けとの摩擦すなわち固体摩擦 $\;R\;$ がある場合を考える。
これは主に腕時計の立姿勢時を解析する場合に用いられる。
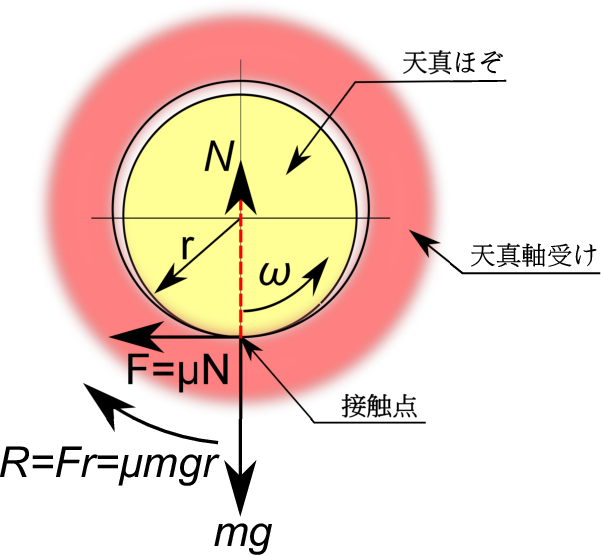
上図はテンプが立姿勢の時の天真ほぞと天真軸受の関係を示す。
天真ほぞと天真軸受は図のように一点のみで接触し、軸受に重力の力$\;mg\;$が鉛直下向きにかかる。$\;m\;$はテンプの質量である。
接触点での摩擦係数を $\;\mu\;$ とすると接触点において天真ほぞは角速度 $\;\omega\;$ とは逆向きに摩擦力$\;F=\mu N=\mu mg\;$を受ける。
ここで$\;N\;$は軸受の垂直抗力で$\;mg\;$と同じ大きさである。これより天真ほぞの半径を $\;r\;$ とすると天真は接触点において
$\;R=Fr=\mu mgr\;$ の摩擦トルクを受けることになる。
さて固体摩擦トルクは$\;R=\mu mgr\;$ と表せたが式が複雑になるため今後これを単に$\;R\;$とおいて解析を進める。
粘性減衰と固体摩擦がある場合の運動方程式の右辺は
$\;-c\frac{d\theta}{dt}-k\theta-(\pm)R\;$となる。復号は$\;\omega=\frac{d\theta}{dt}\;$ >0のとき+、<0のときはーをとる。
復号が付く理由は固体摩擦力が常に $\;\omega\;$ の向きと逆方向であるからである。
そうするとこの場合のテンプの運動方程式は
\begin{eqnarray}
I\frac{d^2\theta}{dt^2}=-c\frac{d\theta}{dt}-k\theta-(\pm) R
\end{eqnarray}
ここで
$\;I\;$:テンワの慣性モーメント
$\;c\;$:粘性摩擦係数
$\;k\;$:ヒゲゼンマイのバネ定数
$\;R\;$:テンワ軸受の固体摩擦トルク
$\;\theta\;$:テンワの振り角
両辺を$\;I\;$で除し右辺を左辺に移項すると
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+\frac{c}{I}\frac{d\theta}{dt}
+\frac{k}{I}\theta\pm\frac{R}{I}=0
\end{eqnarray}
ここで$\;\zeta\;$:粘性減衰比率、$\;\omega_n\;$:固有振動数、$\;\omega_d\;$:減衰系固有振動数 を次のようにおけば
\begin{eqnarray}
&\zeta&=\frac{c}{2\sqrt{Ik}} \nonumber \\
&\omega_n&=\sqrt{\frac{k}{I}} \nonumber \\
&\omega_d&=\sqrt{1-\zeta^2}\;\omega_n \nonumber
\end{eqnarray}
式(2)は
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+2\zeta\omega_n\frac{d\theta}{dt}
+\omega_n^2\theta\pm\frac{R}{I}=0
\end{eqnarray}
となる。ここで
\[\theta_{t=0}=A_0,\;\;\;\;\left(\frac{d\theta}{dt}\right)_{t=0}=0\]
として式(3)をラプラス変換(第5部 数学公式集 5-3-2 ラプラス変換表参照)すると
\begin{eqnarray}
s^2\Theta(s)-s\theta_{t=0}-\left(\frac{d\theta}{dt}\right)_{t=0}+2\zeta\omega_n(s\Theta(s)-\theta_{t=0})+\omega_n^2\Theta(s)\pm\frac{R}{Is}=0
\end{eqnarray}
\begin{eqnarray}
s^2\Theta(s)+2\zeta\omega_ns\Theta(s)+\omega_n^2\Theta(s)=A_0(s+2\zeta\omega_n)-(\pm)\frac{R}{Is}
\end{eqnarray}
すなわち
\begin{eqnarray}
(s^2+2\zeta\omega_ns+\omega_n^2)\Theta(s)=A_0((s+2\zeta\omega_n)-(\pm)\frac{R}{Is}
\end{eqnarray}
変形して
\begin{eqnarray}
\Theta(s)&=&A_0\frac{(s+2\zeta\omega_n)}{s^2+2\zeta\omega_n+\omega_n^2}-(\pm)\frac{R}{Is(s^2+2\zeta\omega_ns+\omega_n^2s)} \nonumber \\
&=&A_0(\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}+\frac{\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2})-(\pm)\frac{R}{I\omega_n^2}\left(\frac{1}{s}-\frac{s+2\zeta\omega_n}{s^2+2\zeta\omega_n+\omega_n^2}\right) \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+
\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\} \nonumber \\ &\;&-(\pm)\frac{R}{I\omega_n^2}\left(\frac{1}{s}-\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}-\frac{\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}\right) \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+\frac{\zeta\omega_n}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\} \nonumber \\ &\;&-(\pm)\frac{R}{I\omega_n^2}\left\{\frac{1}{s}-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}-\frac{\zeta\omega_n}{\omega_d}\frac{\zeta\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\}
\end{eqnarray}
ここで
\begin{eqnarray}
\frac{R}{I\omega_n^2}=\frac{R}{k}=r
\end{eqnarray}
とおいて式(7)をラプラス逆変換(第5部 数学公式集 5-3-2 ラプラス変換表参照)すると
\begin{eqnarray}
\theta&=&A_0e^{-\zeta\omega_n t}\{cos\omega_d t+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t\}-(\pm)r\left[1-e^{-\zeta\omega_n t}\left\{cos\omega_d t+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t\right\}\right] \nonumber \\
&=&A_0e^{-\zeta\omega_n t}\left\{cos\omega_d t+\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t\right\} \nonumber \\
&\;&-(\pm)r\left[1-e^{-\zeta\omega_n t}\left\{cos\omega_d t+\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t\right\}\right] \nonumber \\
&=&A_0\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)-(\pm)r+(\pm)r\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}cos(\omega_d t-\phi)
\end{eqnarray}
整理すると
\begin{eqnarray}
\theta\pm r=(A_0\pm r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
ただし
\begin{eqnarray}
0&\le& t \le \frac{\pi}{\omega_d} \\
\phi&=&tan^{-1}(\frac{\zeta}{\sqrt{1-\zeta^2}}) \\
r&=&\frac{R}{k} \nonumber
\end{eqnarray}
これが粘性減衰と固体摩擦があるときのテンプの自由振動の解である。式(10)の復号は$\;\omega=\frac{d\theta}{dt}\;$ >0のとき+、<0のときはーをとる。
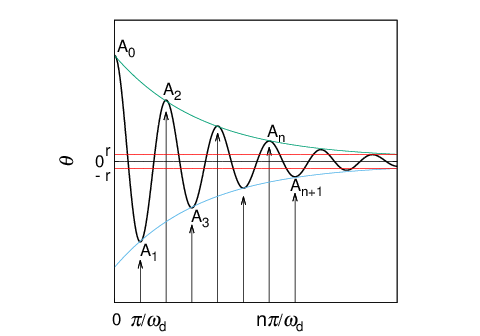
$\;\frac{d\theta}{dt}\;$の符号が変わる$\;\frac{d\theta}{dt}=0\;$のとき、つまり $\;\theta\;$ が極大値、極小値を取るごとに振動の中心が本当の中心から $\;r\;$ だけずれる。
これを図示すると下図のようになる。そして振り角$\;A=\theta\pm r\;$ が $\;r\;$ よりも小さくなったとき振動が停止する。