Next, when the solid friction, ''$R$'' works between the balance pivot and the balance bearing, how it works? This will be used to mainly analyze the vertical position of the wrist watch.
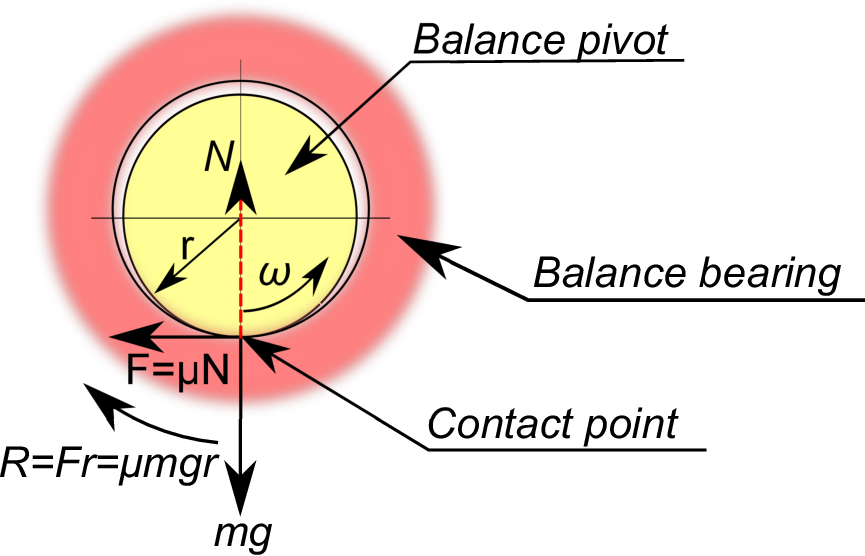
The figure above shows the physical relationship between the balance pivot & balance bearing when the balance is used in the vertical position.
The balance pivot & the balance bearing contact
at the point as shown in the figure above, and the gravity force, ''$mg$'' works vertical downward direction. The ''$m$'' represents the mass of the balance.
Assuming that ''$\mu$'' represents the friction coefficient at the contact point, the balance pivot receives the friction force, ''$F = \mu N = \mu mg$'' at the contact point in the opposite direction of the angular velocity, ''$\omega$''. ''$N$'' represents the vertical drag of the slide bearing which is the same greatness as ''$mg$''.
In other words, the balance staff receives the friction torque, ''$R = Fr =\mu mgr$'' at the contact point, assuming that ''$r$'' represents the radius of the balance pivot. In the meantime, although the solid friction torque can be represented ''$R =\mu mgr$'', this will be simply represented ''$R$'' in our continued analysis from now on due to its complicated equation.
When the viscous damping and the solid friction actually work, the right side of the equation of motion becomes
''$-c d\theta/dt - k\theta - (\pm)R$''.
The plus-minus notation is ''+'' for ''$\omega = d \theta/dt \ge 0$'' and ''-'' for '' $<$ 0''.
The reason for the plus-minus notation is because of the fact that the solid friction force always works in the opposite direction of ''$\omega$''.
Accordingly, in this case, the equation of motion of the balance can be shown in the equation (1).
\begin{eqnarray}
I\frac{d^2\theta}{dt^2}=-c\frac{d\theta}{dt}-k\theta-(\pm) R
\end{eqnarray}
Conditions:
$\;I\;$:Moment of inertia of the balance wheel
$\;c\;$:Viscous damping coefficient
$\;k\;$:Spring constant of hairspring
$\;R\;$:Solid friction torque of balance wheel bearing
$\;\theta\;$:Displacement of balance wheel
Dividing the both sides of the equation by ''$I$'', and transposing the right side to the left side, the equation (1) can be converted to the equation (2).
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+\frac{c}{I}\frac{d\theta}{dt}
+\frac{k}{I}\theta\pm\frac{R}{I}=0
\end{eqnarray}
Defining each of the viscous damping factor, ''$\zeta$'', the natural frequency, ''$\omega_n$'', and the natural frequency of the damping system, ''$\omega_d$'' as follows,
\begin{eqnarray}
&\zeta&=\frac{c}{2\sqrt{Ik}} \nonumber \\
&\omega_n&=\sqrt{\frac{k}{I}} \nonumber \\
&\omega_d&=\sqrt{1-\zeta^2}\;\omega_n \nonumber
\end{eqnarray}
the equation (2) can be converted to the equation (3).
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+2\zeta\omega_n\frac{d\theta}{dt}
+\omega_n^2\theta\pm\frac{R}{I}=0
\end{eqnarray}
Here, assuming the following conditions, taking the Laplace transform of the equation (3), equations (4) can be obtained.
\[\theta_{t=0}=A_0,\;\;\;\;\left(\frac{d\theta}{dt}\right)_{t=0}=0\]
\begin{eqnarray}
s^2\Theta(s)-s\theta_{t=0}-\left(\frac{d\theta}{dt}\right)_{t=0}+2\zeta\omega_n(s\Theta(s)-\theta_{t=0})+\omega_n^2\Theta(s)\pm\frac{R}{Is}=0
\end{eqnarray}
This equation can be converted to the equations (5) & (6).
\begin{eqnarray}
s^2\Theta(s)+2\zeta\omega_ns\Theta(s)+\omega_n^2\Theta(s)=A_0(s+2\zeta\omega_n)-(\pm)\frac{R}{Is}
\end{eqnarray}
\begin{eqnarray}
(s^2+2\zeta\omega_ns+\omega_n^2)\Theta(s)=A_0((s+2\zeta\omega_n)-(\pm)\frac{R}{Is}
\end{eqnarray}
Transforming the equation (6), the equation (7) can be obtained.
\begin{eqnarray}
\Theta(s)&=&A_0\frac{(s+2\zeta\omega_n)}{s^2+2\zeta\omega_n+\omega_n^2}-(\pm)\frac{R}{Is(s^2+2\zeta\omega_ns+\omega_n^2s)} \nonumber \\
&=&A_0(\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}+\frac{\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2})-(\pm)\frac{R}{I\omega_n^2}\left(\frac{1}{s}-\frac{s+2\zeta\omega_n}{s^2+2\zeta\omega_n+\omega_n^2}\right) \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+
\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\} \nonumber \\ &\;&-(\pm)\frac{R}{I\omega_n^2}\left(\frac{1}{s}-\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}-\frac{\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}\right) \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+\frac{\zeta\omega_n}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\} \nonumber \\ &\;&-(\pm)\frac{R}{I\omega_n^2}\left\{\frac{1}{s}-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}-\frac{\zeta\omega_n}{\omega_d}\frac{\zeta\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\}
\end{eqnarray}
Here, assuming the conditions of the equation (8), taking the inverse Laplace transform of the equation (7), the equation (9) can be obtained as a result.
\begin{eqnarray}
\frac{R}{I\omega_n^2}=\frac{R}{k}=r
\end{eqnarray}
\begin{eqnarray}
\theta&=&A_0e^{-\zeta\omega_n t}\{cos\omega_d t+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t\}-(\pm)r\left[1-e^{-\zeta\omega_n t}\left\{cos\omega_d t+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t\right\}\right] \nonumber \\
&=&A_0e^{-\zeta\omega_n t}\left\{cos\omega_d t+\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t\right\} \nonumber \\
&\;&-(\pm)r\left[1-e^{-\zeta\omega_n t}\left\{cos\omega_d t+\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t\right\}\right] \nonumber \\
&=&A_0\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)-(\pm)r+(\pm)r\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}cos(\omega_d t-\phi)
\end{eqnarray}
Assuming that the conditions are specified in the equation (11), sorting out the equation (9) to make it simple, it becomes the equation (10).
\begin{eqnarray}
\theta\pm r=(A_0\pm r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
\begin{eqnarray}
0&\le& t \le \frac{\pi}{\omega_d} \\
\phi&=&tan^{-1}(\frac{\zeta}{\sqrt{1-\zeta^2}}) \\
r&=&\frac{R}{k} \nonumber
\end{eqnarray}
This is the solution of the free vibration of the balance when the viscous damping and the solid friction work. The plus-minus notation of the equation (10) is ''+'' for ''$\omega = d \theta/dt \ge 0$'' and ''-'' for ''$< 0$'' as shown previously.
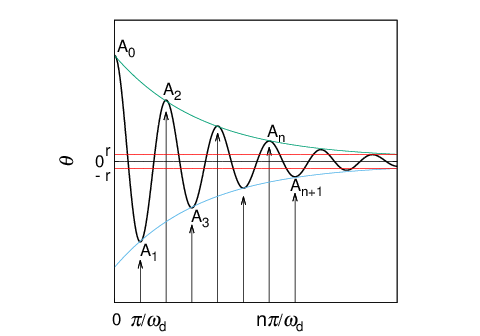
When the plus-minus notation of ''$d \theta/dt$'' is changed at the ''$d\theta/dt =0$'' condition, in other words, at the every maximum & minimum values ''$\theta$'' takes, the center of the vibration is deviated from the real center by ''$r$''. Illustrating this, the figure below can be indicated. The vibration stops when the displacement, ''$A = \theta \pm r$'' becomes smaller than ''$r$''.