第3部 等時性誤差
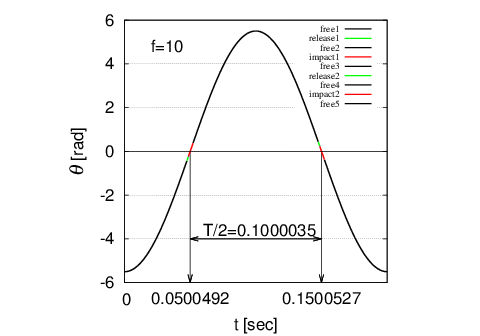
ここでは新たな試みとして4次のルンゲクッタ法を使って振り角$\;\theta\;$を1周期分逐次計算し、 これから周期を読み取って正確な脱進機誤差を算出する。 まずテンプの運動方程式を自由振動期間、ガンギ解除期間、テンプ衝撃期間 に分けて立てると次のようになる。 [自由振動期間] \begin{eqnarray} I\frac{d^2 \theta}{dt^2}=-c\frac{d\theta}{dt}-k\theta-(\pm)R \end{eqnarray}[ガンギ解除期間] \begin{eqnarray} I\frac{d^2 \theta}{dt^2}=-(\pm)S-c\frac{d\theta}{dt}-k\theta-(\pm)R \end{eqnarray}[テンプ衝撃期間] \begin{eqnarray} I\frac{d^2 \theta}{dt^2}=(\pm)M-c\frac{d\theta}{dt}-k\theta-(\pm)R \end{eqnarray}ここで $I$ : テンワの慣性モーメント $c$ : 粘性減衰係数 $k$ : ヒゲゼンマイのバネ定数 $R$ : 天真ほぞの固体摩擦抵抗, $S$ : ガンギ解除時のテンプの負荷トルク $M$ : テンプ衝撃トルク である。復号は$\omega=\frac{d\theta}{dt} \ge 0$のとき+、<0のときはーをとる。 ここで式(1)〜式(3)の両辺を$\;I\;$で除すと [自由振動期間] \begin{eqnarray} \frac{d^2 \theta}{dt^2}=-\omega_n^2(j\frac{d\theta}{dt}+\theta\pm r) \end{eqnarray}[ガンギ解除期間] \begin{eqnarray} \frac{d^2 \theta}{dt^2}=-\omega_n^2(j\frac{d\theta}{dt}+\theta\pm s\pm r) \end{eqnarray}[テンプ衝撃期間] \begin{eqnarray} \frac{d^2 \theta}{dt^2}=-\omega_n^2(j\frac{d\theta}{dt}+\theta-(\pm)m\pm r) \end{eqnarray}ただし \begin{eqnarray} j=\frac{c}{k}\\ r=\frac{R}{k} \\ s=\frac{S}{k}\\ m=\frac{M}{k} \end{eqnarray}である。 ここで \begin{eqnarray} S=\varepsilon M \end{eqnarray}とおくと$\;\varepsilon\;$は解除トルクと衝撃トルクの比を表し脱進機の構造により定まる。 通常のクラブツース型脱進機の場合は$\;\varepsilon\;=\;0.2\;〜\;0.4$である。 ここで $\alpha$=ガンギ解除開始テンプ角度 $\beta$=ガンギ解除終了テンプ角度 $\gamma$=衝撃開始テンプ角度 $\eta$=衝撃終了テンプ角度 を設定し、テンプ1周期を -$A_0$〜$\alpha$ 自由振動期間1 $\alpha$〜$\beta$ ガンギ解除期間1 $\beta$〜$\gamma$ 自由振動期間2 $\gamma$〜$\eta$ テンプ衝撃期間1 $\eta$〜-$\alpha$ 自由振動期間3 -$\alpha$〜-$\beta$ ガンギ解除期間2 -$\beta$〜-$\gamma$ 自由振動期間4 -$\gamma$〜-$\eta$ テンプ衝撃期間2 -$\eta$〜-$A_0$ 自由振動期間5 の9期間に分けて式(4)〜式(6)を4次のルンゲクッタ法により計算する。 脱進機誤差$\;\delta\;$は \begin{eqnarray} \delta=86400\frac{T_0-T}{T}=86400(\frac{2\pi}{\omega_0\;T}-1)=86400(\frac{1}{f\;T/2}-1) \end{eqnarray}で表されるから$\;T/2\;$を$\;\theta\;$のグラフから読み取れば正確な$\;\delta\;$が計算できる。 今回例として$\alpha=-25^\circ$ , $\beta=-15^\circ$ , $\gamma=-13^\circ$ ,$\eta=22^\circ$ , $\varepsilon=0.3$, $M=2.73\times10^{-7}\;[Nm]$,$k=1.184352528\times10^{-6}\;[Nm/rad]$, $I=1.2\times10^{-9}\;[kgm^2]$,$c=8.41\times10^{-11}\;[Nms]$,$R=2.85\times10^{-9}\;[Nm]$, 振動数$f$=10とおいて振り角$\;\theta\;$を計算した結果を 下図に示す。 このときの半周期$\;T/2\;$は下図から$0.1000035\;[sec]$であった。 これより脱進機誤差$\;\delta\;$は式(12)から次のように計算される。 \begin{eqnarray} \delta=86400(\frac{1}{10\times 0.1000035}-1)=-3.023894\;\;[sec/Day] \nonumber \end{eqnarray} 尚、このときの4次のルンゲクッタ法の刻み幅は$1\times10^{-7}$とした。 この場合$\;\theta\;$は$1\times10^{-28}$程度の精度を持つが、今回は$\;\theta\;$が符号を反転させる時間差を読んでいるので 精度は$1\times10^{-6}$である。
|