関数$f(x)$の最大最小値問題を考えるとき一つの方法は関数$f(x)$を$x$で微分して導関数$df(x)/dx$=0となる$x$を見つけることである。
導関数が0になるような$x$に対して関数$f(x)$は最大値、最小値、変曲値のいずれかになり、これは微分法の基礎的な項目である。
これと非常に似たような問題として関数$f(x)$の形によって決まる量$G(x,y,y')$(つまり関数形の関数、これを汎関数と呼ぶ)の
最大最小問題を考えるのが変分法と言われるものである。
汎関数$G$の微小な変化を0にするような関数形に対してその汎関数は最大値、最小値、停留値のいずれかをとることになる。
求めたいのはこのような関数形$f(x)$である。つまり汎関数が最大最小値をとるとき$\delta G=0$である。
いわば変分法は関数による関数の微分というようなものである。
下図は微分法のイメージである。変数$x$を少し変化させると関数$f(x)$の値もほんの少し変わっている。
ただし曲線の形自体は変わっていない。
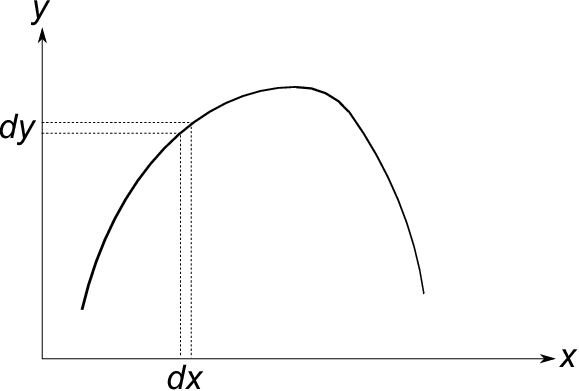
次に変分問題の場合は下図のようになり、$x$の変化に対し変化するのは関数$f(x)$の値ではくて関数$f(x)$の形そのものになる。

変分法を解くにはオイラー方程式を解くという方法がある。汎関数$G\{y\}=\int_a^bf(x,y,y')dx$のように関数$f(x,y,y')$の積分で
定義されているとき、オイラー方程式というものを解けば汎関数に最大最小値を与える$f(x,y,y')$が求まることになる。
今$y=y(x)$という関数があり、関数$f$は$x,y,y'$によって決まる関数とする。
この$\;f\;$の積分によって汎関数$G$が次のように積分の形で与えられる。
\begin{eqnarray}
G[y]=\int_a^bf(x,y,y')dx
\end{eqnarray}
この$G$が最大最小値を持つように関数$f$の関数形を求めるというのが変分問題である。
基本的な考え方は微分と同じで最大最小値の近くでは関数形を少し変えたときの汎関数の変化$\delta G$(これを第一変分と呼ぶ)が
非常に小さいということを利用する。
関数$y(x)$が最初$y_0(x)$という関数だったとし、これに対して任意の関数$H(x)$とある微小な量$\xi$を導入し、次のように$y(x)$を
ほんの少しだけ変形させよう。積分区間の両端では変形がないように$H(x)$には式(3)のような初期条件も与えておく。
\begin{eqnarray}
y(x)&=&y_0(x)+\xi H(x) \\
\frac{\partial y}{\partial \xi}&=&H(x) \nonumber \\
\frac{\partial y'}{\partial \xi}&=&H'(x) \nonumber \\
H(a)&=&H(b)=0
\end{eqnarray}
ここで導入した$\xi$は関数形を変化させるための変数であり、汎関数$G[y]$に最大最小値を与える関数形に対しては、ほんの少し関数形が
変化しても汎関数の変化は非常に小さいはずである。したがって$f(x)$が最大最小値を与えるという条件は次式が成り立つことである。
\begin{eqnarray}
\{\frac{dG[y]}{d\varepsilon}\}_{\varepsilon=0}=0
\end{eqnarray}
そこで式(1)の汎関数を$\xi$で微分し、部分積分の公式(5-2)を使えば
\begin{eqnarray}
\frac{dG}{d\xi}&=&\frac{d}{d\xi}\int_a^bf(x,y,y')dx \nonumber \\
&=&\int_a^b(\frac{\partial f}{\partial y}\frac{\partial y}{\partial \xi}+\frac{\partial f}{\partial y'}\frac{\partial y'}{\partial \xi})dx \nonumber \\
&=&\int_a^b\{\frac{\partial f}{\partial y}H(x)+\frac{\partial f}{\partial y'}H'(x)\}dx \nonumber \\
&=&[\frac {\partial f}{\partial y'}H(x)]_a^b+\int_a^bH(x)\{\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})\}dx \nonumber \\
&=&\int_a^bH(x)\{\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})\}dx
\end{eqnarray}
4行目の
\[[\frac {\partial f}{\partial y'}H(x)]_a^b
\]は初期条件から0になる。
ここで$H(x)$は任意の関数であるから右辺が恒等的に0になるには{ }で括ってある部分が0になる必要がある。
これより汎関数$G$が最大最小値をとるためには
\begin{eqnarray}
\frac{dG}{d\xi}=\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})=0
\end{eqnarray}
となることが必要である。
すなわち
\begin{eqnarray}
\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})=0
\end{eqnarray}
これをオイラーの方程式と呼ぶ。