1-1 Equation of Motion of Pendulum
First principles of mechanical watch & clock are derived from pendulum clock. In the light of history, the simplest and the most accurate mechanical clock is pendulum clock and in order to theoretically analyze mechanical watch & clock, it is fundamental to firstly clarify the motion of pendulum.
Then, as a starter, I would like to formulate an equation of motion, and to work on this.
From the Newton's law, when the mass ''$m$'' object receives the force ''$F$'', acceleration ''$\alpha$'' is generated in proportion to the given force in the same force direction. This can be applied to the moving pendulum as well.
The equation is shown in (1).
\begin{eqnarray}
m\alpha=F
\end{eqnarray}
As shown in the figure below, force of gravity ''$mg$'' applied to the mass in a vertical & downward direction. The force ''$F$'' is defined as ''$-mg\;sin\theta$'' which is the component force of gravity. As the rightward increasing $\theta$ is defined as ''+'', ''-'' is attached as the above.
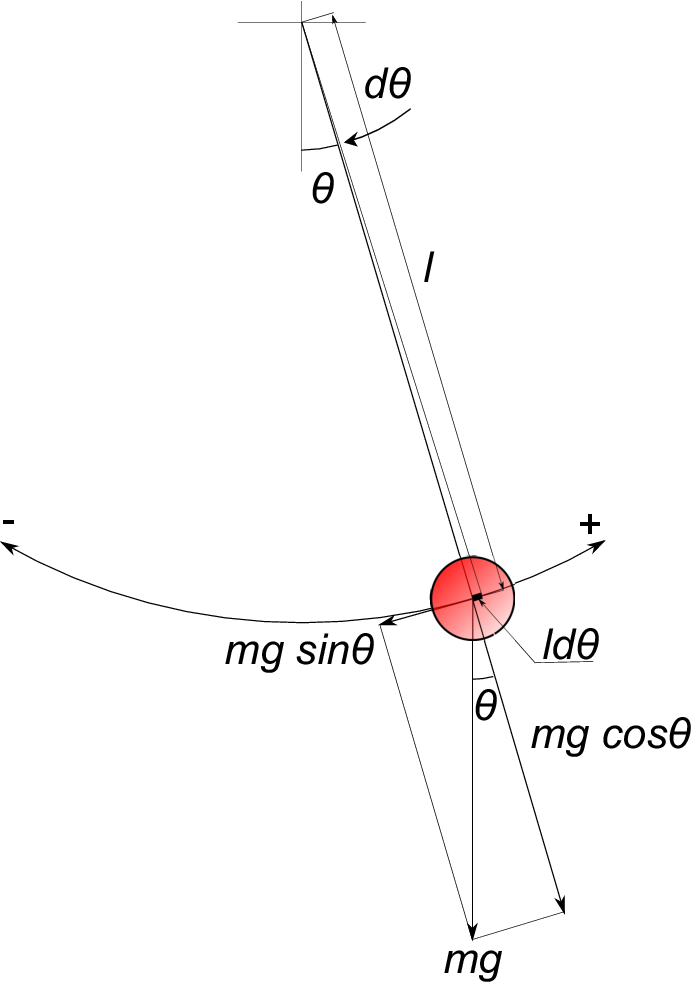
As orthogonal ''$mg\;cos\theta$'' to the motion direction is always balanced with the tensile force of
the thread, no attention is necessary here.
One of the most important things to formulate the equation of motion is to firstly fix the axis of coordinate, along the motion direction of the object.In this case, the circular arc which the pendulum is swinging is the axis of coordinate, and the rightward increasing ''$\theta$'' is defined as ''+''.
Next, left side of the equation is set up with ''$m\alpha=$'', then all forces on the axis of coordinate (on the tangent line in case of the circular arc) to be described at the right side of the equation.
At this time, there should be only ''$-mg\;sin\theta$''.
As formulating the equation of motion itself is the most important thing, it should be convenient to bear that in mind.
Firstly let's find the velocity of the pendulum.
Assuming that the pendulum is now moving rightward, as ''distance divided by time equals velocity'', ''Velocity = Distance / Time'', the minute circular arc length, ''$l\;d\theta$'' at figure above means ''distance'', and the minute time ''$dt$'' means ''time''. Accordingly, velocity ''$v$'' of the pendulum
can be calculated by dividing ''$l\;d\theta$'' by ''$dt$'' (differentiating ''$l\;\theta$'' with respect to ''$t$'').
\begin{eqnarray}
v=\frac{ld\theta}{dt}
\end{eqnarray}
In addition, acceleration ''$\alpha$'' can be obtained by differentiating velocity with respect to time.
\begin{eqnarray}
\alpha=\frac{dv}{dt}=l\frac{d^2\theta}{dt^2}
\end{eqnarray}
Following equation (4) can be then obtained from equation (1).
\begin{eqnarray}
ml\frac{d^2\theta}{dt^2}=-mgsin\theta
\end{eqnarray}
This is the equation of motion of pendulum in its free vibration.
There are various ways to figure out the equation of motion. In this book, I have decided
to use Laplace transform which is appropriate for vibration analysis and comparatively easy to solve. Laplace transform is the method to transform the time-domain ''$t$'' into the complex plane ''$s$''. It is really a simple way to obtain the solution of a differential equation by implementing inverse Laplace transform once again to return back to the time-domain ''$t$'' after transforming the equation of the complex number ''$s$''.
In terms of the proof of Laplace transform, the details are skipped in this book as it is described in many mathematical publications. It should be noted that all you need to do is
just remember the transformation formula described in Section 5 Mathematical Fomulas, 5.3.2 Laplace transform table, so that equation of motion can be automatically solved.
Now, let's solve the equation (4) taking Laplace transform.
Dividing the both sides of the equation (4) by ''$ml$'',
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta
\end{eqnarray}
When “$\theta$” is small, the equation (6) is formed.
\begin{eqnarray}
sin\theta\approx\theta
\end{eqnarray}
Accordingly, the equation (7) can be obtained.
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta
\end{eqnarray}
Then, taking the Laplace transform of both sides of the equation, under the following initial conditions,
\[\theta_{t=0}=A_0,\;\;\;\;\left(\frac{d\theta}{dt}\right)_{t=0}=0\]
the equation (8) can be obtained. (Refer to Section 5 Mathematical Formulas 5-3-2)
\begin{eqnarray}
&\;&s^2\Theta(s)-s\theta_{t=0}-\left(\frac{d\theta}{dt}\right)_{t=0}=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&s^2\Theta(s)-sA_0=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&(s^2+\frac{g}{l})\Theta(s)=sA_0 \nonumber \\
&\;&\Theta(s)=\frac{sA_0}{(s^2+\frac{g}{l})}
\end{eqnarray}
The equation (9) can be obtained by taking the inverse Laplace transform here.
(Refer to Section 5 Mathematical Formulas 5-3-2)
\begin{eqnarray}
\theta=A_0cos\sqrt{\frac{g}{l}} t
\end{eqnarray}
\begin{eqnarray}
\omega_n=\pi\;f=\sqrt{\frac{g}{l}}
\end{eqnarray}
At this point, $\omega_n$ represents natural frequency. The natural frequency means
that the repeated number of times of vibration rate per unit time multiplied by angle $2\pi$ rad. of a period. In the case of watch & clock, the frequency is counted twice a shuttle.
The natural frequency will be accordingly ''$\pi f$'' as shown in the equation(10).
It should be careful not to confuse this with angular velocity ''$\omega$''.
As a result, the equation (11) can be obtained from the equations (9) & (10).
\begin{eqnarray}
\theta=A_0cos\omega_n t
\end{eqnarray}
Period ''$T$'' is shown in the equation (12).
\begin{eqnarray}
T=\frac{2\pi}{\omega_n}={2\pi}\sqrt{\frac{l}{g}}
\end{eqnarray}
The equation (11) is the solution during the pendulum continues to make the free vibration.
Period ''$T$'' becomes constant regardless of amplitude ''$A_0$'' of the pendulum.
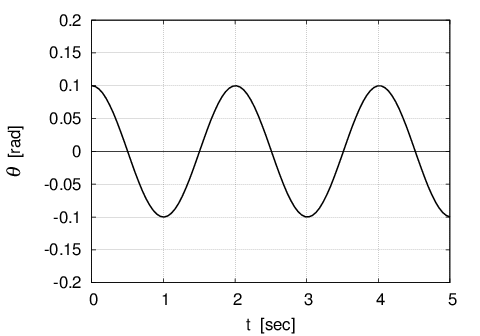
The figure below is a graphic representation of the equation (11).
Each condition as an example is as follows:
''$l$'' = $1 [m]$, ''$g$'' =$ 9.8 [m/s^2 ]$, ''$A_0$'' = $0.1 [rad]$
This represents the motion status of the pendulum during the time after putting the pendulum at the right (''+'' direction) edge and then releasing the hand at that exact point of time at the time ''zero''. In this case, natural frequency ''$\omega_n$'' and period ''$T$'' can be shown as follows:
\begin{eqnarray}
\omega_n&=&\sqrt{\frac{g}{l}}=\sqrt{\frac{9.8}{1}}=3.1305\;[rad/s] \nonumber \\
T&=&\frac{2\pi}{\omega_n}=2\pi\sqrt{\frac{l}{g}}=2\times \pi \times \sqrt{\frac{1}{9.8}}=2.0071\;[sec] \nonumber
\end{eqnarray}