振り子の角速度$\;\omega\;$を求めてみよう。1-1で求めた振り子の運動方程式の解は
\begin{eqnarray}
\theta=A_0cos\sqrt{\frac{g}{l}} t=A_0cos\omega_n t
\end{eqnarray}
であった。
式(1)を$\;t\;$で微分すれば
\begin{eqnarray}
\omega&=&\frac{d\theta}{dt} \nonumber \\
&=&-A_0\sqrt{\frac{g}{l}}sin{\sqrt{\frac{g}{l}}t}=-A_0\omega_n sin \omega_n t
\end{eqnarray}
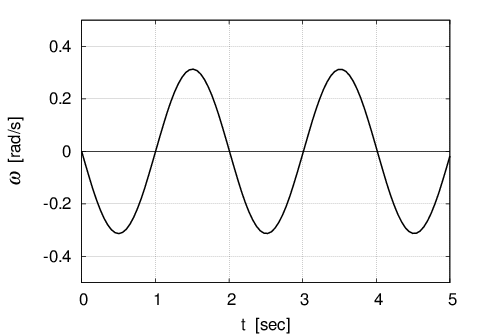
これをグラフにすると図のようになる。角速度$\;\omega\;$は初速0から徐々にマイナス方向に大きくなり
$l=1[m] , g=9.8 [m/s^2]$, $A_0=0.1 [rad]$のとき
\begin{eqnarray}
t=\frac{T}{4}=\frac{\pi}{2}\sqrt{\frac{l}{g}}=0.5018\;[sec] \nonumber
\end{eqnarray}
で負の極大値となる周期運動となる。
式(2)に
\begin{eqnarray}
t=\frac{\pi}{2}\sqrt{\frac{l}{g}} \nonumber
\end{eqnarray}
を代入すると次のように負の極大値が求められる。
\begin{eqnarray}
\omega_{max}=-A_0\sqrt{\frac{g}{l}}=-A_0\omega_n=-0.313\;[rad/s]
\end{eqnarray}
これより角速度$\;\omega\;$の最大値(絶対値)は振り角$\;A_0\;$の$\;\omega_n\;$倍になっていることがわかる。