Let's obtain the angular velocity, ''$\omega$''.
The solution to the free vibration of the pendulum is represented by the following equation (1) as in clause 1-1.
\begin{eqnarray}
\theta&=&A_0 cos \sqrt{\frac{g}{l}} t
\end{eqnarray}
Differentiating the equation (1) with respect to ''$t$'', the equation (2) can be obtained.
\begin{eqnarray}
\omega&=&\frac{d\theta}{dt} \nonumber \\
&=&-A_0\sqrt{\frac{g}{l}}sin{\sqrt{\frac{g}{l}}t}=-A_0\omega_n sin \omega_n t
\end{eqnarray}
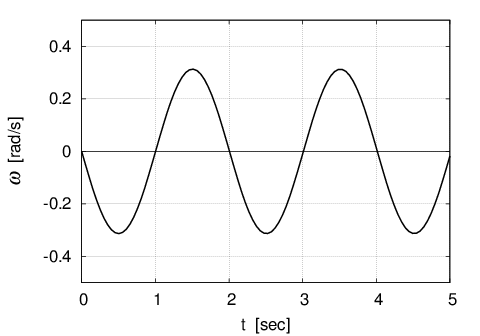
Then, making a graph of this equation (2), it becomes the figure below.
The angular velocity, ''$\omega$'' gets gradually greater in minus direction from initial velocity zero, and the following ''$t$'' represents the periodic motion resulting in the negative maximum value in the case of ''$l$'' = $1 [m]$, ''$g$'' =$ 9.8 [m/s^2 ]$, ''$A_0$'' = $0.1 [rad]$.
\begin{eqnarray}
t=\frac{T}{4}=\frac{\pi}{2}\sqrt{\frac{l}{g}}=0.5018\;[sec] \nonumber
\end{eqnarray}
Substituting the ''$t$'' equation into the equation (2), the following negative maximum value can be obtained.
\begin{eqnarray}
\omega_{max}=-A_0\sqrt{\frac{g}{l}}=-A_0\omega_n=-0.313\;[rad/s]
\end{eqnarray}
Looking at this equation (3), maximum value (absolute value) of angular velocity, $\omega_{max}$ represents $\omega_n$ times of the amplitude, $A_0$.