Although the equation (1), the solution obtained in clause 1-1 is the ''$cos$'' form, the ''$sin$'' form can be alternatively obtained by changing the initial condition in solving the equation of motion.
\begin{eqnarray}
\theta=A_0 cos \omega_n t
\end{eqnarray}
The equation of motion of pendulum is represented by the equation (2) as in clause 1-1.
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l} \theta
\end{eqnarray}
In order to obtain the solution of the ''$sin$'' form, the initial condition in taking Laplace transform is changed as follows:
\[\theta_{t=0}=0\;\;\;\;\;\;\;\; \left(\frac{d\theta}{dt}\right)_{t=0}=\omega_0\]
Then, taking the Laplace transform of the equation (2), the equation (3) can be obtained.
\begin{eqnarray}
&\;&s^2\Theta(s)-s\theta_{t=0}-\left(\frac{d\theta}{dt}\right)_{t=0}=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&s^2\Theta(s)-\omega_0=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&(s^2+\frac{g}{l})\Theta(s)=\omega_0 \nonumber \\
&\;&\Theta(s)=\frac{\omega_0}{(s^2+\frac{g}{l})}
\end{eqnarray}
Next, taking the inverse Laplace transform, the equation (4) can be obtained.
\begin{eqnarray}
\theta=\omega_0\sqrt{\frac{l}{g}}\;sin\sqrt{\frac{g}{l}} t=\frac{\omega_0}{\omega_n}\;sin\;\omega_n t
\end{eqnarray}
Then, making a graph of this equation (4), it becomes the figure below.
It should be noted that initial velocity ''$\omega_0$'' of angular velocity is the value of ''$\omega_{max}$'',
$0.313\;[rad/s]\;$which comes from the ''$cos$'' form above. Accordingly, it is the same amplitude
as that of the ''$cos$'' form as a matter of course.
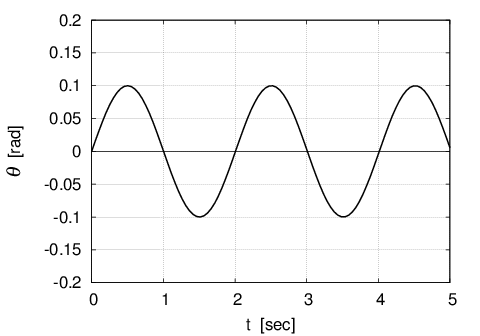
The figure abobe represents the status of motion of the pendulum at a later time when the pendulum is located at the vertical & downward directions, and the initial velocity ''$\omega_0$'' of angular velocity was given to the rightward under the condition ''time zero'' in that instant.