実際の振り子運動は空気抵抗や支点での何らかのエネルギー散逸により減衰運動となる。一般的にこれらの減衰は粘性減衰と呼ばれ、
数学的取り扱いが容易なこともあって粘性減衰力$\;f_d\;$を次式のようにあらわす。
ただし、本当の減衰メカニズムは未だよく判っていないことが多い。
\begin{eqnarray}
f_d=c\frac{d\theta}{dt}
\end{eqnarray}
ここで$\;c\;$は粘性減衰係数と呼ばれる。
つまり円弧上を運動する振り子は速度に比例した抵抗力を運動方向と逆向きに受ける。
仮に支点や糸に減衰があったとしてもすべてこれらを振り子に対する抵抗力$\;f_d\;$として考える。
すなわち今、振り子が右方向へ運動しているとすれば図のように重力の分力$\;mg\;sin\theta\;$と同じ方向に抵抗力$\;f_d\;$が働く。
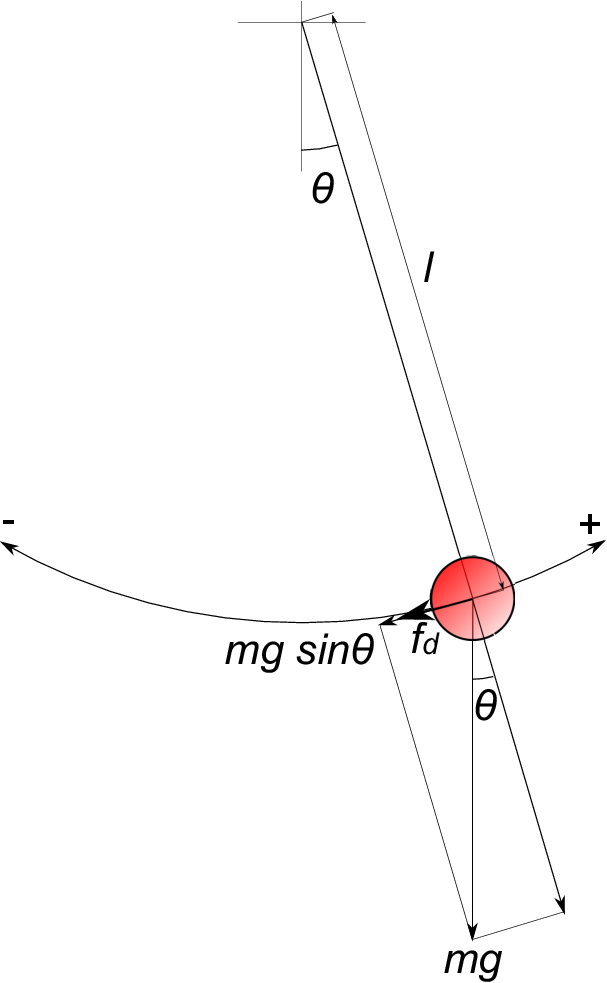
これを式で表せば
\begin{eqnarray}
ml\frac{d^2\theta}{dt^2}&=&-mg\theta-f_d \nonumber \\
&=&-mg\theta-c\frac{d\theta}{dt}
\end{eqnarray}
両辺を$\;ml\;$で除し右辺を左辺に移項すれば
\begin{eqnarray}
\frac{d^2\theta}{dt^2}&+\frac{c}{ml}\frac{d\theta}{dt}+\frac{g}{l}\theta=0
\end{eqnarray}
これが粘性減衰があるときの振り子の運動方程式である。
ここで$\;\zeta\;$:粘性減衰比率、$\;\omega_n\;$:固有振動数、$\;\omega_d\;$:減衰系固有振動数
を次のように定義する。
\begin{eqnarray}
&\zeta&=\frac{c}{2m\sqrt{gl}} \\
&\omega_n&=\sqrt{\frac{g}{l}} \\
&\omega_d&=\sqrt{1-\zeta^2}\;\omega_n
\end{eqnarray}
そうすると式(3)は次のように書き換えられる。
\begin{eqnarray}
\frac{d^2\theta}{dt^2}&+2\zeta\omega_n\frac{d\theta}{dt}+\omega_n^2\theta=0
\end{eqnarray}
それではこれをラプラス変換(第5部 数学公式集 5-3-2 ラプラス変換表参照)を用いて解いてみよう。
式(7)を初期条件 \[\theta_{t=0}=A_0 ,\;\;\;\;(\frac{d\theta}{dt})_{t=0}=0\]のもとにラプラス変換すると
\begin{eqnarray}
s^2\Theta(s)-s\theta_{t=0}-(\frac{d\theta}{dt})_{t=0}+2\zeta\omega_n(s\Theta(s)-\theta_{t=0})+\omega_n^2\Theta(s)=0\;\;\;\;\;
\end{eqnarray}
\begin{eqnarray}
s^2\Theta(s)+2\zeta\omega_ns\Theta(s)+\omega_n^2\Theta(s)=A_0(s+2\zeta\omega_n)
\end{eqnarray}
すなわち
\begin{eqnarray}
(s^2+2\zeta\omega_ns+\omega_n^2)\Theta(s)=A_0(s+2\zeta\omega_n)
\end{eqnarray}
変形して
\begin{eqnarray}
\Theta(s)&=&A_0\frac{(s+2\zeta\omega_n)}{s^2+2\zeta\omega_ns+\omega_n^2s} \nonumber \\
&=&A_0\left(\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2s}+\frac{\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2s}\right) \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\} \nonumber \\
&=&A_0\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}+\frac{\zeta\omega_n}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\}
\end{eqnarray}
ラプラス逆変換し、三角関数の合成公式(第5部 数学公式集 5-1-9 三角関数の合成公式参照)を使えば
\begin{eqnarray}
\theta&=&A_0e^{-\zeta\omega_n t}\{cos\omega_d t+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t\} \nonumber \\
&=&A_0e^{-\zeta\omega_n t}\{cos\omega_d t+\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t\} \nonumber \\
&=&A_0\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
ただし
\begin{eqnarray}
\phi=tan^{-1}(\frac{\zeta}{\sqrt{1-\zeta^2}})
\end{eqnarray}
これが粘性減衰があるときの振り子の自由振動の解である。これをグラフにすると下の図のようになる。
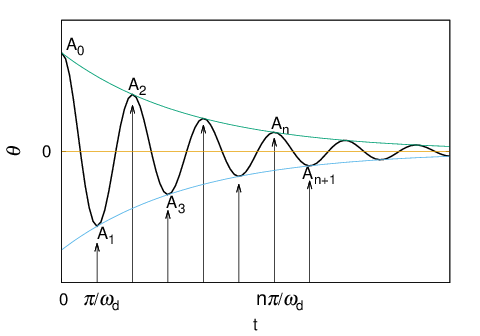
これより減衰する振り子は半振動(時計用語の1振動)
\begin{eqnarray}
t=\frac{\pi}{\omega_d}
\end{eqnarray}
ごとに極大極小値をとることがわかる。
式(12)の右辺の$\;cos\;$の中には$\;\phi\;$が入っているので直感的に極大極小の周期が判りにくいので念のため式(12)を微分しておく。
極大極小値をとるときは
\begin{eqnarray}
\frac{d\theta}{dt}=0
\end{eqnarray}
となるはずである。
式(12)を$t$で微分すると(第5部 数学公式集 微分基本公式 5-2-2 関数の積の微分参照)
\begin{eqnarray}
\frac{d\theta}{dt}&=&-\frac{A_0}{\sqrt{1-\zeta^2}}\{\zeta\omega_n e^{-\zeta\omega_n t}cos(\omega_d t-\phi)+\omega_d\;e^{-\zeta\omega_n t}sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{A_0}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\omega_n\{\zeta\; cos(\omega_d t-\phi)+\sqrt{1-\zeta^2}\;sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{A_0\;\omega_n}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\;sin\omega_d t
\end{eqnarray}
式(16)が0になるのは\[t=n\frac{\pi}{\omega_d}\]のときであるからこのとき$\;\theta\;$は極大極小値を持つことが証明された。
次に実際に極大極小値を求めてみよう。
1回目の極小値$\;|A_1|\;$は式(12)に式(14)を代入して
\begin{eqnarray}
|A_1|&=&-|A_0|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos(\pi-\phi) \nonumber \\
&=&|A_0|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos\phi \nonumber \\
&=&|A_0|e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
同様に2回目の極大値$\;|A_2|\;$は式(12)の$\;A_0\;$を$\;A_1\;$に置き換えて\[t=\frac{\pi}{\omega_d}\]を代入すれば
\begin{eqnarray}
|A_2|&=-&|A_1|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos(\pi-\phi) \nonumber \\
&=&|A_1|\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos\phi \nonumber \\
&=&|A_1|e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
$\;|A_0|\;$と$\;|A_2|\;$の差を$\;\Delta A\;$とすると
\begin{eqnarray}
\Delta A&=&|A_0|-|A_2| \nonumber \\
&=&|A_0|-|A_1|\{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\} \nonumber \\
&=&|A_0|-|A_0|e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\} \nonumber \\
&=&|A_0|(1-e^{-\frac{2\zeta\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&\approx&|A_0|\frac{2\zeta\pi}{\sqrt{1-\zeta^2}}
\end{eqnarray}
最後の式は$\;e\;$のべき乗をテイラー展開(第5部 数学公式集 5-4 テイラー展開参照)で近似した結果である。
同様に$\;N\;$回目の極大値$\;A_N\;$は
\begin{eqnarray}
|A_N|=|A_0|e^{-\frac{N\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
$\;N+n\;$回目の極大値$\;|A_{N+n}|\;$は
\begin{eqnarray}
|A_{N+n}|=|A_0|e^{-\frac{(N+n)\zeta\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
となり、$\;N\;$回目の極大値$\;|A_N|\;$から$\;n\;$振動後の振り角損失$\;\Delta A_n\;$は次のようになる。
\begin{eqnarray}
\Delta A_n&=&|A_N|-|A_{N+n}| \nonumber \\
&=&|A_0|e^{-\frac{N\zeta\pi}{\sqrt{1-\zeta^2}}} -|A_0|e^{-\frac{(N+n)\zeta\pi}{\sqrt{1-\zeta^2}}} \nonumber \\
&=&|A_0|e^{-\frac{N\zeta\pi}{\sqrt{1-\zeta^2}}} (1-e^{-\frac{n\zeta\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&=&|A_N|(1-e^{-\frac{n\zeta\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&\approx&\frac{n\zeta\pi}{\sqrt{1-\zeta^2}}|A_N|
\end{eqnarray}
したがって任意の振り子1周期(2振動)での振り角損失$\;\Delta A\;$は
\begin{eqnarray}
\Delta A&\approx&\frac{2\zeta\pi}{\sqrt{1-\zeta^2}}A \nonumber \\
&=&\frac{c}{2ml}T_d A
\end{eqnarray}
ただし$\;T_d\;$は減衰があるときの振り子の周期で次式で表される。
\begin{eqnarray}
T_d=\frac{2\pi}{\omega_d}
\end{eqnarray}