振動系の良さを示す指標として$\;Q\;$値(Quality factor)というものがある。これは次式にて定義することができる。
\begin{eqnarray}
Q=2\pi\frac{E}{\Delta E}
\end{eqnarray}
ここで $\;E\;$:振り子の保有エネルギー
$\;\Delta E\;$:振り子1周期での消費エネルギー
ここで振り子の保有エネルギーを求めるためにバネによるモデルを考える。
図のようにバネを距離$\;x\;$だけ伸ばしたとき、復元力$\;F\;$はバネ定数を$\;k\;$とおくと
\begin{eqnarray}
F=-kx
\end{eqnarray}
と表される。
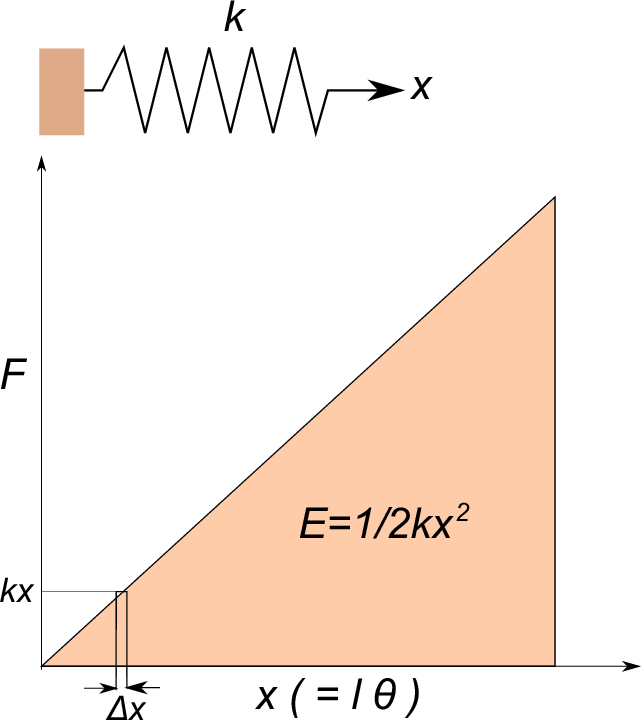
このときバネの保有エネルギーはエネルギー(力×距離)=$\;kx \times x\;$を$\;\Delta x\;$毎に0〜$\;x\;$まで寄せ集めた(積分した)
ものだから図の三角形の面積と同じになる。すなわちバネの保有エネルギー$\;E\;$は
\begin{eqnarray}
E=&\frac{1}{2}kx^2
\end{eqnarray}
で表される。
振り子の場合は$\;F=-mg\theta\;$だったからこれを円弧上の移動距離$\;x\;$で表すと
\begin{eqnarray}
F=-\frac{mg}{l}\;x
\end{eqnarray}
となる。
すなわち振り子をバネに置き換えるとバネ定数$\;k=mg/l\;$と等価となる。
そうすると振り子の保有エネルギー$\;E\;$はバネの場合と同じように
\begin{eqnarray}
E=\frac{1}{2}\frac{mg}{l}x^2
\end{eqnarray}
となる。振り角$\;A\;$を使えば$\;x=lA\;$となるので結局、振り角$\;A\;$で振動する振り子の保有エネルギー$\;E\;$は
\begin{eqnarray}
E=\frac{1}{2}mglA^2
\end{eqnarray}
となる。
式(6)を$\;A\;$で微分すると
\begin{eqnarray}
\Delta E=mglA\Delta A
\end{eqnarray}
式(6)(7)を式(1)に入れれば
\begin{eqnarray}
Q=\frac{\pi A}{\Delta A}
\end{eqnarray}
これに1-4で求めた式(23) $\;\Delta A=\frac{c}{2ml}T_dA\;$ を代入すると
\begin{eqnarray}
Q&=&\frac{\pi}{\frac{cT_d}{2ml}} \nonumber \\
&=&\frac{\pi m l f}{c} \\
&=&\frac{\sqrt{1-\zeta^2}}{2\zeta} \\
&\approx&\frac{1}{2\zeta}
\end{eqnarray}
ただし$\;f\;$は時計における振動数(周波数の2倍)である。
式(9)より$\;Q\;$値は振り子の錘が重いほど、糸の長さは長いほど、振動数は多いほど大きな数値となる。
一方、$\;Q\;$値は粘性減衰係数$\;c\;$が小さいほど大きくなる。
また式(11)は$\;\zeta\;$が小さいとき成り立ち、$\;Q\;$値はほぼ粘性減衰比率の2倍の逆数と一致することがわかる。
一般的な大型振り子時計の場合、$\;Q\;$値は数千のオーダーに達するので粘性減衰比率は$8\times 10^{-5}$〜$2.5\times10^{-4}$程度の値となる。
一般的に粘性減衰係数$\;c\;$は不明なことが多いので$\;Q\;$値を計算するには振り子を自由振動させて振り角が半減するまでの
時間を測定することが多い。
振り角が半減するまでの時間を$\;t_1\;$とすると1-4の式(4)(5)から$\;\zeta\omega_n=c/(2ml)\;$だから
\[
0.5=e^{-\zeta \omega_n t_1}=exp\{-c\; t_1/2ml\} \nonumber \\
\]
とおいて両辺の対数をとれば
\begin{eqnarray}
\ln{0.5}&=&-\frac{c\; t_1}{2ml} \nonumber \\
&=&-\frac{\pi f t_1}{2Q}
\end{eqnarray}
これより$\;t_1\;$を実測すると$\;c\;$や$\;\zeta\;$が求まり、$\;Q\;$値を次式で計算することが出来る。
\begin{eqnarray}
Q=-\frac{\pi f t_1}{2\ln{0.5}}=2.26618\;f\;t_1
\end{eqnarray}
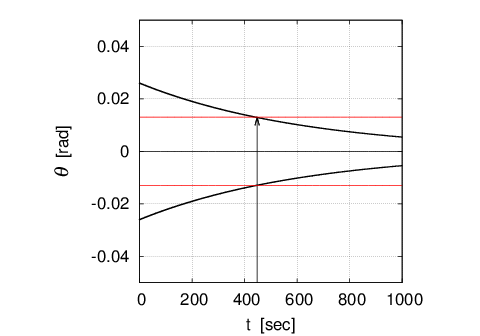
下図に$\;Q\;$値の測定例を示す。これは振り角の初期条件を$A_0=0.026\; [rad]$とし、振り子を自由振動させて
振り角の極大値のみを時間とともに測定した結果である。極小値は極大値を反転して作成したものである。
測定条件は振り子の質量$m=0.15\; [kg]$ 、糸の長さ$l=1.02\; [m]、$振り子錘の形状は円柱形で直径は$0.015\; [m]$、
長さ$0.1\;[m]$である。温度は$25$℃であった。
振動数$\;f\;$は150回の振動に要した時間を測定し(結果は151.01sec)これを1秒当たりに換算し$\;f=0.9933\;$を得た。
$\;f\;$の値は理論的には次式で与えられるが実質的な糸の長さ$\;l\;$は不明なことが多いので実際には振動数を計測して
糸の長さを逆算する方が良いと思われる。
\begin{eqnarray}
f=\frac{1}{\pi}\sqrt{\frac{g}{l}}
\end{eqnarray}
振動数より糸の長さを修正すると
\begin{eqnarray}
l'=\frac{g}{\pi^2f^2}=1.006\; [m]
\end{eqnarray}
となる。ただし重力加速度$\;g=9.8\;[m/s^2]\;$とする。
このとき下図に示すように約450秒で振り子の振り角が半減した。
これより、この振り子の$\;Q\;$値は式(13)より
\begin{eqnarray}
Q=2.26618 \times 0.993 \times 450=1013
\end{eqnarray}
のように求めることが出来る。尚、このときの粘性減衰係数 $\;c\;$ を実験結果から逆算すると$\;c=0.00047\;[Ns]\;$となった。
これを等価粘性減衰係数と呼ぶ。