Quality factor is the performance indicator of the oscillation system.
This can be defined as the following equation (1).
\begin{eqnarray}
Q=2\pi\frac{E}{\Delta E}
\end{eqnarray}
''$E$'' & ''$\Delta E$'' are defined as follows:
$E$: Retaining energy of the pendulum
$\Delta E$: Energy consumption in a period of the pendulum
Then, considering the spring related model in order to figure out the retaining energy of the pendulum, as shown in the figure below, when the spring is expanded by the distance ''$x$'', the restoring force, ''$F$'' is described as the equation (2) assuming that its spring constant, ''$k$''.
\begin{eqnarray}
F=-kx
\end{eqnarray}
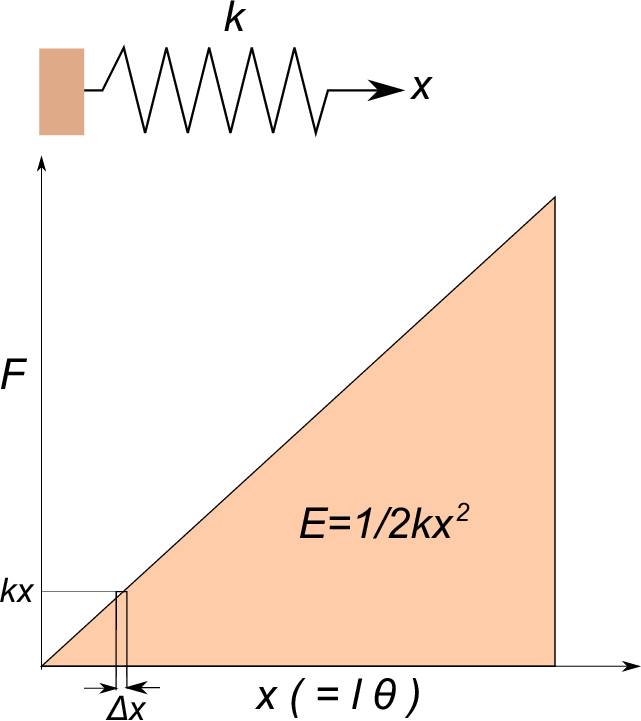
The retaining energy of the spring is represented that the energy equals force ''$kx$'' by distance ''$x$''. This energy is what is integrating the energy (''$kx$'' by ''$x$'') with respect to
$\Delta x$ each from $0$ to $x.$ It becomes the same triangle area of the figure above. Therefore, retaining energy of the spring, ''$E$'' can be described as the equation (3).
\begin{eqnarray}
E=&\frac{1}{2}kx^2
\end{eqnarray}
In case of the pendulum, it was described as ''$F=-mg\theta$''. Accordingly, describing this as the moving distance, ''$x$'' on the circular arc, it can be converted to the equation (4).
\begin{eqnarray}
F=-\frac{mg}{l}\;x
\end{eqnarray}
In other words, when the pendulum is replaced with the spring, it is equivalent with the spring constant, ''$k=mg/l$''. The retaining energy of the pendulum, ''$E$'' can be converted to the equation (5) which is the same as that of the spring.
\begin{eqnarray}
E=\frac{1}{2}\frac{mg}{l}x^2
\end{eqnarray}
With the use of the amplitude, ''$A$'', it is described as ''$x = lA$''. Retaining energy, ''$E$'' of the vibrating pendulum in its displacement, ''$A$'' can be eventually converted to the equation (6).
\begin{eqnarray}
E=\frac{1}{2}mglA^2
\end{eqnarray}
Differentiating the equation (6) with respect to ''$A$'', the equation (7) can be obtained.
\begin{eqnarray}
\Delta E=mglA\Delta A
\end{eqnarray}
Substituting the equations (6 & 7) to the equation (1), it becomes the equation (8).
\begin{eqnarray}
Q=\frac{\pi A}{\Delta A}
\end{eqnarray}
Substituting further the equation (9) obtained in 1-4 to this equation (8), the equations (10), (11) & (12) can be obtained.
\begin{eqnarray}
\Delta A&=&\frac{c}{2ml}T_d A \\
Q&=&\frac{\pi}{\frac{cT_d}{2ml}} \nonumber \\
&=&\frac{\pi m l f}{c} \\
&=&\frac{\sqrt{1-\zeta^2}}{2\zeta} \\
&\approx&\frac{1}{2\zeta}
\end{eqnarray}
Be noted that ''$f$'' of the equation (10) is the watch frequency which means 2 times of general frequency.
According to the equation (10), the Quality factor becomes greater numeric as mass of the pendulum is heavier, the thread is longer and the frequency is greater.
In addition, Quality factor becomes greater as viscous damping coefficient, ''$c$'' is lesser.
The equation (12) is based on the condition that ''$\zeta$'' is small. The Quality factor is accordingly known that it approximately corresponds to the inverse number of 2 times of the viscous damping factor.
In case of the large pendulum clock, as the Quality factor will usually reach several thousands numeric, the viscous damping factor will be around $8\times10^{-5}$〜$2.5\times10^{-4}$.
As the viscous damping coefficient ''$c$'' does not generally seem clear, practical approach to figure it out is to mostly make the pendulum oscillating freely and to measure the time its amplitude reduction by half.
In terms of the ''$t_1$'' for the time for reducing the amplitude by half, the following equation can be introduced from ''$\zeta \omega_n = c/(2ml)$'' based on the equations (4) & (5) obtained in 1-4.
\[
0.5=e^{-\zeta \omega_n t_1}=exp\{-c\; t_1/2ml\} \nonumber \\
\]
Then, equation (13) can be described by taking the logarithm of both sides of this equation above.
\begin{eqnarray}
\ln{0.5}&=&-\frac{c\; t_1}{2ml} \nonumber \\
&=&-\frac{\pi f t_1}{2Q}
\end{eqnarray}
Accordingly, parameters ''$c$'' and ''$\zeta$'' can be obtained by actually measuring ''$t_1$'', and using with the equation (13), the Quality factor can be calculated by the following equation (14).
\begin{eqnarray}
Q=-\frac{\pi f t_1}{2\ln{0.5}}=2.26618\;f\;t_1
\end{eqnarray}
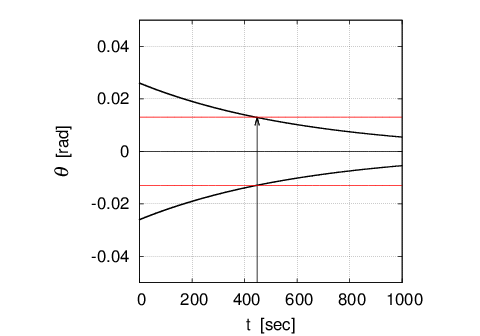
This is the measurement result of only the maximum value of the displacement of the pendulum in the time course during free vibration of the pendulum, under the initial condition of the amplitude, ''$A_0$'' = $0.026\;[rad]$. Minimum value in this chart was generated by reversing the maximum value.
The measurement conditions are as follows:
-mass of the pendulum: $m = 0.15 \;[kg]$
-length of the thread: $l = 1.02 \;[m]$
-shape of the pendulum mass: $cylindrical$
-diameter / length: $0.015 [m] / 0.1 \;[m]$
-ambient temperature: $25 \;[^\circ C] $
The frequency ''$f $'' can be obtained by measuring the time for taking 150 times of the vibration and by converting it to the numerical data per second. The actual measurement result of the time was 151.01 seconds which was proven ''$f = 0.9933$''. The ''$f$'' value can be theoretically obtained with the following equation (15) . But, as the substantial thread length does not seem clear in many cases, it will be appropriate, in practice, to measure the frequency ''$f$'' and to calculate backward the thread length.
\begin{eqnarray}
f=\frac{1}{\pi}\sqrt{\frac{g}{l}}
\end{eqnarray}
Based on this ''$f$'', the compensated thread length can be obtained as shown in the equation (16), assuming that acceleration of gravity, ''$g = 9.8 [m/s^2]$''.
\begin{eqnarray}
l'=\frac{g}{\pi^2f^2}=1.006\; [m]
\end{eqnarray}
The figure below shows that the amplitude of the pendulum was reduced by half in about 450 seconds. Accordingly, the Quality factor of this pendulum can be obtained as shown in the equations (14 &17).
\begin{eqnarray}
Q=2.26618 \times 0.993 \times 450=1013
\end{eqnarray}
As for the viscous damping coefficient, ''$c$'' at this time, ''$c = 0.00047 \;[Ns]$'' can be obtained by calculating backward based on the experimental result. This is called as the equivalent viscous damping coefficient.