サイクロイドとはある直線上で円板を滑ることなく転がしたときに円板上のある一点が描く軌跡である。
この曲線は時計の歯車にも使われている。
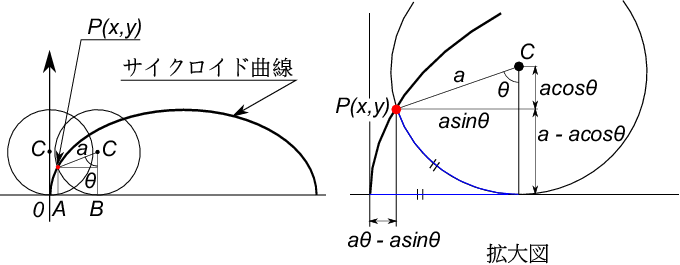
図から判るように、サイクロイド曲線は半径$\;a\;$の円$\;C\;$が$\;x\;$軸に接しながら回転するとき、
その半径上に固定された点$\;P\;$の軌跡となる。式で表せば
\begin{eqnarray}
x&=&a(\theta-sin\theta) \\
y&=&a(1-cos\theta)
\end{eqnarray}
となる。
次に下の図のように2つのサイクロイド曲線の間に挟まれた振り子を考える。サイクロイドを描いた円の半径を $\;a\;$ とするとき、
振り子の糸の長さを $\;4a\;$ にとると振り子自身が描く軌跡も$\;x\;$軸を $\;2a\;$ だけオフセットしたサイクロイドになる。
下の図で言うと青い線が振り子の軌道である。このときこの振り子をサイクロイド振り子と呼ぶ。

単振り子の場合はその周期$\;T\;$は1-6の振り子の厳密解のように振り角$\;A_0\;$の関数であったが、
サイクロイド振り子の場合は振り角に依らず一定となる。これを証明してみよう。
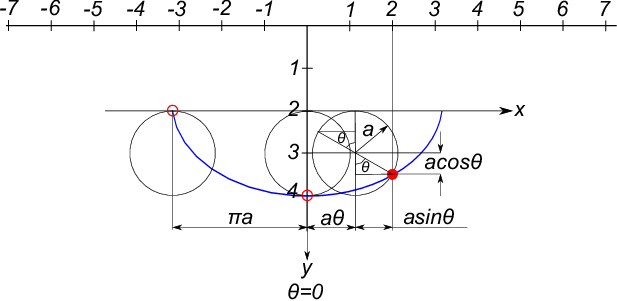
上図から振り子がとるサイクロイド軌道は
\begin{eqnarray}
x&=&a\theta+a sin\theta \nonumber \\
&=&a(\theta+sin\theta) \\
y&=&a+acos\theta \nonumber \\
&=&a(1+cos\theta)
\end{eqnarray}
で表される。これは式(1)(2)で$\;\pi+\theta\;$を$\;\theta\;$に置き換え$\;y\;$軸を$\;\pi a\;$だけシフトしたものに等しい。
尚、$\;\theta\;$はここでは振り子の振り角ではなく振り角に対応したころがり円の回転角度である。
式(3)(4)を$\;\theta\;$で微分すると
\begin{eqnarray}
\frac{dx}{d\theta}&=&a(1+cos\theta) \\
\frac{dy}{d\theta}&=&-asin\theta
\end{eqnarray}
であるからサイクロイド曲線上の微小長さを$\;ds\;$とすると
\begin{eqnarray}
ds&=&\sqrt{dx^2+dy^2}=\sqrt{a^2(1+cos\theta)^2+a^2sin^2\theta}\;d\theta \nonumber \\
&=&a\sqrt{1+2cos\theta+cos^2\theta+sin^2\theta}\;d\theta \nonumber \\
&=&a\sqrt{2}\sqrt{1+cos\theta}\;d\theta
\end{eqnarray}
となる。ここで振り子のエネルギー保存則から
\begin{eqnarray}
\frac{1}{2}mv^2=mg(y-y_0)
\end{eqnarray}
が成り立つ。ただし$\;y_0\;$は振り子の初期位置の$\;y\;$座標である。$\;\theta_0\;$を振り子の初期角度に対応した
ころがり円の回転角とすれば次式が成り立つ。
\begin{eqnarray}
\frac{1}{2}mv^2&=&mg\{a(1+cos\theta)-a(1+cos\theta_0)\} \nonumber \\
&=&mga(cos\theta-cos\theta_0) \nonumber \\
v&=&\sqrt{2ga(cos\theta-cos\theta_0)}
\end{eqnarray}
一方、
\begin{eqnarray}
v&=&\frac{ds}{dt}=\frac{a\sqrt{2}\sqrt{1+cos\theta}\;d\theta}{dt} \nonumber \\
&=&\sqrt{2ga(cos\theta-cos\theta_0)}
\end{eqnarray}
これから
\begin{eqnarray}
dt=\sqrt{\frac{a}{g}}\sqrt{\frac{1+cos\theta}{cos\theta-cos\theta_0}}d\theta
\end{eqnarray}
振り子の1/4の周期$\;T/4\;$は$\;dt\;$ を0から$\;T/4\;$まで積分したものであり、この間振り子はころがり角$\;\theta=0\;$から
$\;\theta=\theta_0\;$まで変化するから
\begin{eqnarray}
\int_0^{T/4}dt=\frac{T}{4}=\int_0^{\theta_0}\sqrt{\frac{a}{g}}\sqrt{\frac{1+cos\theta}{cos\theta-cos\theta_0}}d\theta
\end{eqnarray}
ここで三角関数の半角公式(第5部 数学公式集 5-1-6)から
\begin{eqnarray}
cos\frac{\theta}{2}&=&\sqrt{\frac{1+cos\theta}{2}} \\
cos\theta&=&2cos^2\frac{\theta}{2}-1
\end{eqnarray}
式(12)に式(13)(14)を使えば
\begin{eqnarray}
\frac{T}{4}&=&\sqrt{\frac{a}{g}}\int_0^{\theta_0}\frac{cos\frac{\theta}{2}}{\sqrt{cos^2\frac{\theta}{2}-cos^2\frac{\theta_0}{2}}}\;d\theta \nonumber \\
&=&\sqrt{\frac{a}{g}}\int_0^{\theta_0}\frac{cos\frac{\theta}{2}}{\sqrt{sin^2\frac{\theta_0}{2}-sin^2\frac{\theta}{2}}}\;d\theta
\end{eqnarray}
ここで次のような変数変換を行う。
\begin{eqnarray}
u=\frac{sin\frac{\theta}{2}}{sin{\frac{\theta_0}{2}}}
\end{eqnarray}
微分して
\begin{eqnarray}
\frac{du}{d\theta}&=&\frac{cos\frac{\theta}{2}}{2sin{\frac{\theta_0}{2}}} \nonumber \\
d\theta&=&\frac{2sin{\frac{\theta_0}{2}}}{cos\frac{\theta}{2}}du
\end{eqnarray}
式(15)を式(16)(17)を使って整理すると
\begin{eqnarray}
\frac{T}{4}&=&2\sqrt{\frac{a}{g}}\int_0^1\frac{du}{\sqrt{1-u^2}}
\end{eqnarray}
ここで$\;u=sin\phi\;$とおけば
\begin{eqnarray}
\frac{du}{d\phi}=cos\phi \nonumber \\
du=cos\phi \;d\phi
\end{eqnarray}
式(18)は次のようになる。
\begin{eqnarray}
\frac{T}{4}&=&2\sqrt{\frac{a}{g}}\int_0^{\pi/2}\frac{cos\phi}{cos\phi}\;d\phi \nonumber \\
&=&2\sqrt{\frac{a}{g}}[\phi]_0^{\pi/2} \nonumber \\
&=&\pi \sqrt{\frac{a}{g}}
\end{eqnarray}
すなわち周期$\;T\;$は
\begin{eqnarray}
T&=&2\pi\sqrt{\frac{4a}{g}} \\
&=&2\pi\sqrt{\frac{l}{g}}
\end{eqnarray}
となり、かくしてサイクロイド振り子の等時性が証明された。これは17世紀にオランダの物理学者ホイヘンスが発見したことから
ホイヘンスの振り子とも呼ばれている。