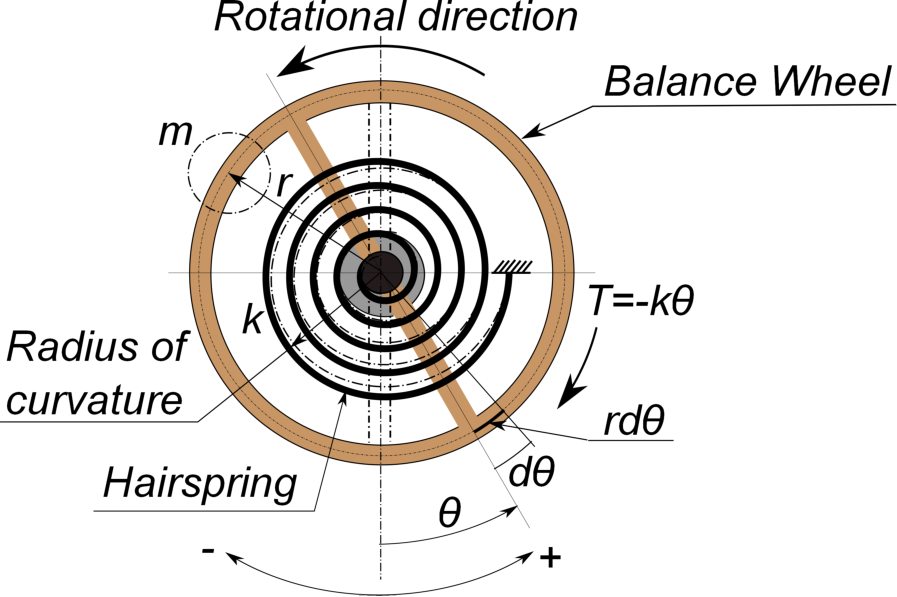
The wrist watch makes the oscillation of the constant period using the balance in place of the pendulum. This is based on the mechanism that makes the reciprocating rotational motion as well as the pendulum by fixing the mass which is the balance wheel in the center part of the spring called as the hairspring. The outer end of the hairspring is fixed.
The figure below shows the situation that the balance wheel is rotated by ''$\theta$'' degrees in the counterclockwise.
In terms of the rotational direction of the balance wheel, deciding the ''+'' for the counterclockwise, the hairspring will change the shape so that the radius of curvature can be enlarged. Then, as the hairspring intends to return back to the previous position, the restoring torque is generated at the balance wheel. Inversely, when the balance wheel rotates clockwise direction, the hairspring will change the shape so that the radius of curvature can be got smaller. At this moment, the hairspring also intends to return back to the previous position as well, the restoring torque is also generated at the balance wheel.
This restoring torque is in proportion to the rotation angle, ''$\theta$'' degrees of the balance wheel.
In this situation, the equation of ''$T$ (the restoring torque)$ = - k\theta$'' can be derived. ''$k$'' of this equation is called as ''spring constant''. In case of the pendulum and the balance, the restoring force is accordingly gravity and the spring constant of the hairspring respectively.
Now, deriving the equation of motion of the balance, back to the Newton's law, equation (1).
\begin{eqnarray}
m\alpha=F
\end{eqnarray}
Multiplying the distance, ''$r$'' at the both sides of the equation (1), the equation (2) can be obtained. As ''$F_r$'' represents '' Force $\times$ distance (Force by distance)'', this represents the torque, ''$T$''.
\begin{eqnarray}
mr\alpha=Fr=T
\end{eqnarray}
In the firure above, the speed, ''$v$'' at the radius of gyration assuming that the mass, ''$m$'' of the balance wheel converged at a point, can be obtained by differentiating the moving distance, ''$rd\theta$'' with respect to the time, as shown in the equation (3) which is the same as that of the pendulum.
\begin{eqnarray}
v=r\frac{d\theta}{dt}
\end{eqnarray}
The acceleration, ''$\alpha$'' can be obtained by differentiating the equation (3) further with respect to the time as shown in the equation (4).
\begin{eqnarray}
\alpha=r\frac{d^2 \theta}{dt^2}
\end{eqnarray}
Substituting this to the equation (2), the equation (5) can be obtained.
\begin{eqnarray}
mr^2\frac{d^2 \theta}{dt^2}&=&T
\end{eqnarray}
Here, note the equation (6) whose ''$I$'' represents the moment of inertia\index{moment of inertia} describing the value of the difficulty in movement of the physical object.
\begin{eqnarray}
I=mr^2
\end{eqnarray}
Accordingly, the equation (5) can be converted to the equation (7) which is very important equation describing the Newton's law in the rotating system.
\begin{eqnarray}
I\frac{d^2 \theta}{dt^2}=T
\end{eqnarray}
As for the equation of motion of the rotating system, all you need to do is firstly describe the following term to the left side of the equation ,
\[I \frac{d^2 \theta}{dt^2}=\]
and to write down the all of the torque factors to the right side of the equation as the same manner in case of the pendulum.
In the figure above, the restoring torque ''$T$'' represents ''$-k\theta$''. Accordingly, the equation of motion can be shown in the equation (8) when the balance is doing the free vibration.
\begin{eqnarray}
I\frac{d^2 \theta}{dt^2}=-k\theta
\end{eqnarray}
Dividing the both sides of the equation by ''$I$'', the moment of inertia, the equation (8) can be converted to the equation (9)
\begin{eqnarray}
\frac{d^2 \theta}{dt^2}=-\frac{k}{I}\theta
\end{eqnarray}
With the following assumption,
\[\theta_{t=0}=A_0,\;\;\;\;\left(\frac{d \theta}{dt}\right)_{t=0}=0\]
taking the Laplace transform of both sides of the equation (9), equation (10) can be obtained.
\begin{eqnarray}
&\;&s^2\Theta(s)-s\theta_{t=0}-\left(\frac{d\theta}{dt}\right)_{t=0}=-\frac{k}{I}\Theta(s) \nonumber \\
&\;&s^2\Theta(s)-sA_0=-\frac{k}{I}\Theta(s) \nonumber \\
&\;&(s^2+\frac{k}{I})\Theta(s)=sA_0 \nonumber \\
&\;&\Theta(s)=\frac{sA_0}{(s^2+\frac{k}{I})}
\end{eqnarray}
Taking the inverse Laplace transform, the equation (11) can be obtained.
\begin{eqnarray}
\theta=A_0cos\sqrt{\frac{k}{I}}t=A_0cos\omega_n t
\end{eqnarray}
Note that ''$\omega_n$'' means the natural frequency of the balance, and it is represented in the equation (12).
\begin{eqnarray}
\omega_n=\pi\;f=\sqrt{\frac{k}{I}}
\end{eqnarray}
The period, ''T'' can be shown in the equation (13).
\begin{eqnarray}
T=\frac{2\pi}{\omega_n}=2\pi \sqrt{\frac{I}{k}}
\end{eqnarray}
The equation (11) is the solution in case of the free vibration of the balance.
Comparing this with the equations (9) & (12) in clause 1-1 , the differences are only [ ''$g$→$k$'' & ''$l$→$I$'' ] which is completely the same shape as that of the pendulum.
In addition, indicating the solution in the form of the ''$sin$'', as well as the case of the pendulum, the equation (14) can be obtained, assuming that ''$\omega_0$'' represents the initial velocity of the angular velocity.
\begin{eqnarray}
\theta=\frac{\omega_0}{\omega_n}\;sin\;\omega_n t
\end{eqnarray}