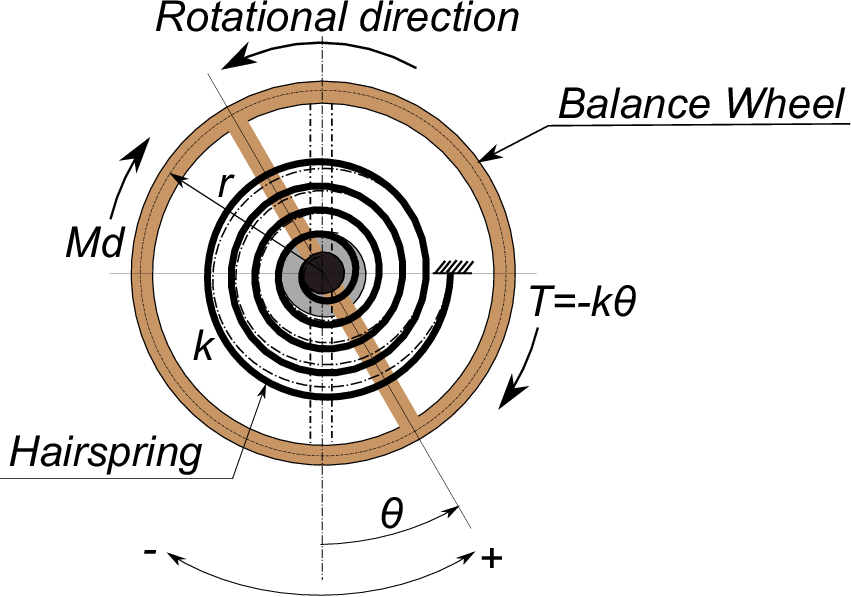
Next, as shown in the figure below, in terms of the equation of motion of the balancce when the viscous damping torque, ''$M_d$'' such as the air resistance etc. works, ''$M_d$'' can be shown in the equation (1), assuming that ''$c$'' represents the viscous damping coefficient as well as the case of the pendulum.
\begin{eqnarray}
M_d=c\frac{d\theta}{dt}
\end{eqnarray}
Accordingly, the equation of motion of the balance can be obtained as shown in the equation (2) .
\begin{eqnarray}
I\frac{d^2 \theta}{dt^2}&=&-k\theta-M_d \nonumber \\
&=&-k\theta-c\frac{d\theta}{dt}
\end{eqnarray}
Dividing the both sides of the equation by ''$I$'', and transposing the right side to the left side, the equation (3) can be indicated.
\begin{eqnarray}
\frac{d^2 \theta}{dt^2}+\frac{c}{I}\frac{d\theta}{dt}+\frac{k}{I}\theta=0
\end{eqnarray}
Equations (4)(5) & (6) are the definitions of the viscous damping factor, ''$\zeta$'', the natural frequency, ''$\omega_n$'', and the natural frequency of the damping system, ''$\omega_d$'' respectively.
\begin{eqnarray}
&\zeta&=\frac{c}{2\sqrt{Ik}} \\
&\omega_n&=\sqrt{\frac{k}{I}} \\
&\omega_d&=\sqrt{1-\zeta^2}\;\omega_n
\end{eqnarray}
Based on the definitions above, the equation (3) becomes the equation (7), completely the same as that of the pendulum 1-4.
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+2\zeta\omega_n\frac{d\theta}{dt}
+\omega_n^2\theta=0
\end{eqnarray}
Obtaining the solution in the same manner as done in the case of the pendulum 1-4, the equation
(8) can be derived as well, assuming that ''$\phi$'' is defined in the equation (9).
\begin{eqnarray}
\theta=A_0\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
\begin{eqnarray}
\phi=tan^{-1}(\frac{\zeta}{\sqrt{1-\zeta^2}})
\end{eqnarray}
This is the solution of the free vibration of the balance when the viscous damping works.
In other words, when the viscous damping works, the displacement of the balance can be shown in the completely same equation as that of the displacement of the pendulum.