固体摩擦があるときのテンプの運動方程式は2-3より次式で表される。
\begin{eqnarray}
I\frac{d^2\theta}{dt^2}=-c\frac{d\theta}{dt}-k\theta-(\pm) R
\end{eqnarray}
ここで
$\;I\;$: テンワの慣性モーメント
$\;c\;$: 粘性減衰係数
$\;k\;$: ヒゲゼンマイのバネ定数
$\;R\;$: テンワ軸受けの固体摩擦トルク
$\;\theta\;$: テンワの振り角
両辺を$\;I\;$で除し右辺を左辺に移項すると
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+\frac{c}{I}\frac{d\theta}{dt}+\frac{k}{I}\theta\pm\frac{R}{I}=0
\end{eqnarray}
ここで$\;\zeta\;$:粘性減衰比率、$\;\omega_n\;$:固有振動数、$\;\omega_d\;$:減衰系固有振動を次のようにおけば
\begin{eqnarray}
&\zeta&=\frac{c}{2\sqrt{Ik}} \\
&\omega_n&=\sqrt{\frac{k}{I}} \\
&\omega_d&=\sqrt{1-\zeta^2}\omega_n
\end{eqnarray}
式(2)は
\begin{eqnarray}
\frac{d^2\theta}{dt^2}+2\zeta\omega_n\frac{d\theta}{dt}+\omega_n^2\theta\pm\frac{R}{I}=0
\end{eqnarray}
ここで
\[\theta_{t=0}=0,\;\;\;\;\left(\frac{d\theta}{dt}\right)_{t=0}=\omega_0\]
として式(6)をラプラス変換(第5部 数学公式集 5-3-2 ラプラス変換表参照)すると
\begin{eqnarray}
s^2\Theta(s)-s\theta_{t=0}-(\frac{d\theta}{dt})_{t=0}+2\zeta\omega_n(s\Theta(s)-\theta_{t=0})+\omega_n^2\Theta(s)\pm\frac{R}{Is}=0
\end{eqnarray}
\begin{eqnarray}
s^2\Theta(s)+2\zeta\omega_ns\Theta(s)+\omega_n^2\Theta(s)=\omega_0-(\pm)\frac{R}{Is}
\end{eqnarray}
すなわち
\begin{eqnarray}
(s^2+2\zeta\omega_ns+\omega_n^2)\Theta(s)=\omega_0-(\pm)\frac{R}{Is}
\end{eqnarray}
変形して
\begin{eqnarray}
\Theta(s)&=&\frac{\omega_0}{s^2+2\zeta\omega_n+\omega_n^2}-(\pm)\frac{R}{Is(s^2+2\zeta\omega_ns+\omega_n^2s)} \nonumber \\
&=&\frac{\omega_0}{s^2+2\zeta\omega_ns+\omega_n^2}-(\pm)\frac{R}{I\omega_n^2}\left(\frac{1}{s}-\frac{s+2\zeta\omega_n}{s^2+2\zeta\omega_n+\omega_n^2}\right) \nonumber \\
&=&\frac{\omega_0}{\{(s+\zeta\omega_n)^2+\omega_d^2\}}-(\pm)\frac{R}{I\omega_n^2}\left(\frac{1}{s}-\frac{s+\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}-\frac{\zeta\omega_n}{s^2+2\zeta\omega_n s+\omega_n^2}\right) \nonumber \\
&=&\frac{\omega_0}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)} \nonumber \\
&\;&\;\;\;\;\;-(\pm)\frac{R}{I\omega_n^2}\left\{\frac{1}{s}-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2)}-\frac{\zeta\omega_n}{\omega_d}\frac{\zeta\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2)}\right\}
\end{eqnarray}
ここで
\begin{eqnarray}
\frac{R}{I\omega_n^2}=\frac{R}{k}=r
\end{eqnarray}
とおいてラプラス逆変換(第5部 数学公式集 5-3-2 ラプラス変換表参照)すると
\begin{eqnarray}
\theta&=&\frac{\omega_0}{\omega_d}e^{-\zeta\omega_n t}sin\omega_d t-(\pm)r\{1-e^{-\zeta\omega_n t}(cos\omega_dt+\frac{\zeta\omega_n}{\omega_d}sin\omega_d t)\} \nonumber \\
&=&\frac{\omega_0}{\sqrt{1-\zeta^2}\omega_n}e^{-\zeta\omega_n t}sin\omega_d t-(\pm)r\pm re^{-\zeta\omega_n t}cos\omega_dt \pm re^{-\zeta\omega_n t}\frac{\zeta}{\sqrt{1-\zeta^2}}sin\omega_d t \nonumber \\
&=&\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}\{\frac{\omega_0}{\omega_n}\pm r\zeta\}sin\omega_dt\pm re^{-\zeta\omega_n t}cos\omega_dt-(\pm)r \nonumber \\
&=&\frac{e^{-\zeta \omega_n t}}{\sqrt{1-\zeta^2}}\{[\frac{\omega_0}{\omega_n}\pm r \zeta]sin\omega_dt\pm r\sqrt{1-\zeta^2}\;cos\omega_dt\}-(\pm)r \nonumber \\
&=&\frac{e^{-\zeta \omega_n t}}{\sqrt{1-\zeta^2}}\sqrt{\{[\frac{\omega_0}{\omega_n}\pm r\zeta]^2+(r\sqrt{1-\zeta^2})^2\}}\;sin(\omega_dt+\phi)-(\pm)r \nonumber \\
&=&\frac{e^{-\zeta \omega_n t}}{\sqrt{1-\zeta^2}}\sqrt{(\frac{\omega_0}{\omega_n}-r)^2+\frac{2r\omega_0}{\omega_n}\{1\pm\zeta\}}\;sin(\omega_dt+\phi)-(\pm)r
\end{eqnarray}
整理すると
\begin{eqnarray}
\theta \pm r=\frac{e^{-\zeta \omega_n t}}{\sqrt{1-\zeta^2}}\sqrt{(\frac{\omega_0}{\omega_n}-r)^2+\frac{2r\omega_0}{\omega_n}\{1(\pm)\zeta\}}\;sin(\omega_dt+\phi)
\end{eqnarray}
ただし
\begin{eqnarray}
0&\le& t \le \frac{\pi}{\omega_d} \\
\phi&=&tan^{-1}\{\frac{r\sqrt{1-\zeta^2}}{\omega_0/\omega_n\pm r\zeta}\} \\
r&=&\frac{R}{k} \nonumber
\end{eqnarray}
である。
最大振り角$\;A_1\;$は$\;t=\pi/2\omega_d\;$のときに次式で表される。
\begin{eqnarray}
A_1=\frac{e^{-\zeta \omega_n \pi/(2\omega_d)}}{\sqrt{1-\zeta^2}}\sqrt{(\frac{\omega_0}{\omega_n}-r)^2+\frac{2r\omega_0}{\omega_n}\{1+\zeta\}}-r
\end{eqnarray}
これよりテンワの角速度の初速$\;\omega_0\;$および$\;r\;$が判れば式(16)からテンワの振り角が計算出来る。$\;r=0\;$のときは式(13)で$\;r=0\;$とおけばよいから次のように表される。
\begin{eqnarray}
\theta=\frac{e^{-\zeta \omega_n t}}{\sqrt{1-\zeta^2}}\frac{\omega_0}{\omega_n}sin\omega_dt
\end{eqnarray}
これをグラフで表すと図のようになる。ただし例として$\omega_0=82.3 [rad/s]$、$Q(\approx \frac{1}{2\zeta})$=400、振動数5とした。
最大振り角$\;A_0\;$は$\;t=\pi/2\omega_d\;$のときに次式で表される。ここで$\;\zeta \ll 1\;$であるから
\begin{eqnarray}
A_0=\frac{e^{-\zeta \omega_n\;\pi/2\omega_d}}{\sqrt{1-\zeta^2}}\frac{\omega_0}{\omega_n}\approx \frac{\omega_0}{\omega_n}
\end{eqnarray}
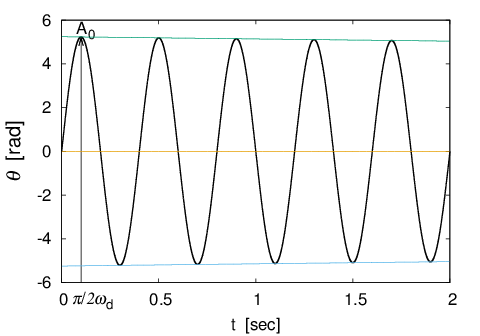
実際はテンワの振り角を315度(=5.5$rad$)程度にしたいので
\begin{eqnarray}
A_0&=&\frac{\omega_0}{\omega_n}=5.5 \\
\omega_0&=&5.5\times \omega_n \nonumber \\
&=&5.5\times \pi f \nonumber \\
&=&17.28\times f
\end{eqnarray}
ここで$\;f\;$は振動数である。つまり毎秒5振動の時計なら衝撃によるテンワの角速度の初速$\omega_0=86.4\;[rad/s]$、
6振動なら$\omega_0=103.68\;[rad/s]$、8振動なら$\omega_0=138.24\;[rad/s]$、10振動なら$\omega_0=172.8\;[rad/s]$のとき
テンワの最大振り角は約315度となる。