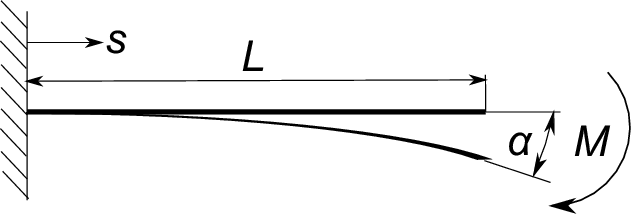
先ず下図のような直線梁の先端にモーメントが加わる場合の先端の傾斜角$\;\alpha\;$を求めてみよう。
ここでモーメント$\;M\;$を受けて撓んだ状態の梁の微小部分を2番目の図に示す。
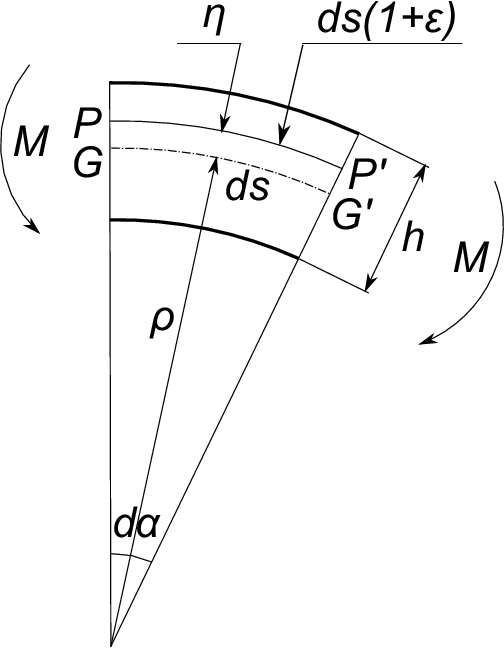
上図で梁は曲げモーメント$\;M\;$を受けて曲率半径$\;\rho\;$に変形しているものとする。
曲線$\;GG'\;$は梁の中立軸でモーメントを受けてもその長さは変わらない。
中立軸から距離$\;\eta\;$の部分の曲線$\;PP'\;$の長さは中立軸よりも外側にあるので引っ張り応力を受けて長さが伸びる。
曲線$\;PP'\;$が元の長さから$\;(1+\varepsilon)\;$倍に伸びたとき、ひずみ$\;\varepsilon\;$は次のようになる。
\begin{eqnarray}
\frac{PP'}{GG'}=\frac{\rho+\eta}{\rho}\;\;\;\;\;\;\;\;\;\;\varepsilon=\frac{\eta}{\rho}
\end{eqnarray}
この繊維に生ずる軸方向の垂直応力$\;\sigma\;$は$\;E\;$を梁の材質のヤング率として次のように表される。
\begin{eqnarray}
\sigma=E\varepsilon=E\frac{\eta}{\rho}
\end{eqnarray}
曲げモーメント$\;M\;$は応力$\;\sigma\;$に微小面積を掛けて力とし、これに中立軸からの距離を掛けて梁の断面全体で
足し合わせたものだから
\begin{eqnarray}
M=\int_A \sigma \eta dA=\frac{E}{\rho}\int_A \eta^2dA
\end{eqnarray}
となる。ここで$\int_A \eta^2dA=I$(断面2次モーメント)とおくと
\begin{eqnarray}
M=\frac{EI}{\rho}\;\;\;\;\;\;\;\;\;\;\frac{1}{\rho}=\frac{M}{EI}
\end{eqnarray}
となる。微小部分の傾斜角$\;d\alpha\;$は$\;ds=\rho d\alpha\;$だから
\begin{eqnarray}
d\alpha=\frac{ds}{\rho}=\frac{M}{EI}ds
\end{eqnarray}
これを$\;s=0\;$から$\;s=L\;$まで積分すれば先端の傾斜角$\;\alpha\;$は次のようになる。
\begin{eqnarray}
\alpha=\int_0^L\frac{ds}{\rho}=\frac{ML}{EI}
\end{eqnarray}
下図のような曲がり梁においても梁の先端に曲げモーメントのみが加わる場合には先端の傾斜角$\;\alpha\;$は
直線梁と同じ結果となる。
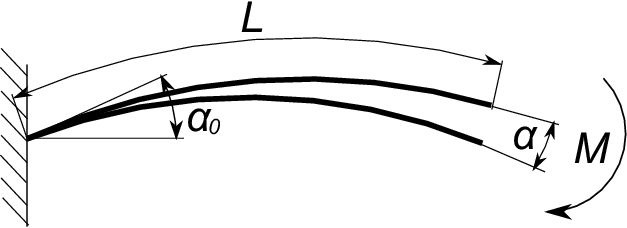
先端に力を加える場合にはこの力による梁の各断面のモーメント分布が直線梁と曲がり梁とでは
異なるのでたわみの様子は異なるが、モーメントだけを加える場合には梁の各断面に働くモーメントが
同じになるので先端の傾斜角も同じ結果となる。
ただし初期傾斜角$\;\alpha_0\;$がある曲がり梁の場合、先端の傾斜角は次式のようになる。
\begin{eqnarray}
\alpha=\alpha_0+\int_0^L\frac{ds}{\rho}=\alpha_0+\frac{ML}{EI}
\end{eqnarray}
ここで曲がり梁先端の初期傾斜角$\;\alpha_0\;$からの変位を$\;\alpha\;$と置きなおせば
\begin{eqnarray}
\alpha=\alpha_0+\frac{ML}{EI}-\alpha_0=\frac{ML}{EI}
\end{eqnarray}
となり結局式(6)と同じ結果となる。
これよりゼンマイの場合の先端の傾斜角は直線梁のときと同じように式(6)で表される。
したがってゼンマイの発生するトルク$\;M\;$は
\begin{eqnarray}
M=\frac{EI}{L}\alpha
\end{eqnarray}
となる。長方形断面の断面2次モーメントは幅$\;b\;$,厚み$\;h\;$とおけば
\begin{eqnarray}
I=\frac{bh^3}{12}
\end{eqnarray}
だからこれを式(9)に代入すればゼンマイトルク$\;M\;$は次式で表される。
\begin{eqnarray}
M=\frac{Ebh^3}{12L}\alpha
\end{eqnarray}
バネ定数$\;k\;$は
\begin{eqnarray}
k=\frac{Ebh^3}{12L}
\end{eqnarray}
となる。
式(11)をグラフで表すと下図の黒線ようになる。これよりゼンマイトルクはゼンマイがほどけるにしたがって
直線的に減少することになる。
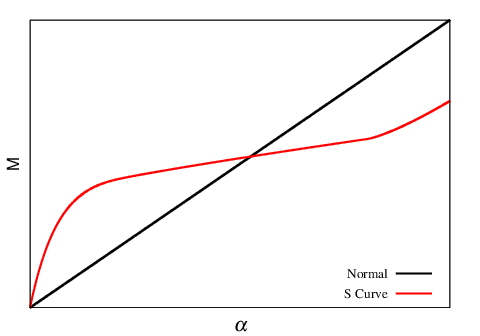
実際には動力用ゼンマイではゼンマイを$S$字状に加工することにより図の赤線のようにトルクを平均化させる
工夫をするのが一般的である。