図に示すように天真の回転中心を座標原点にとり任意の方向に$\;x,y\;$軸をとる。
天真へのヒゲの取り付け位置すなわちヒゲ玉の位置からヒゲの長さに沿って距離$\;s\;$をとる。
変形前のヒゲの形は
\begin{eqnarray}
x=x(s)\;\;\;\;\;\;\;\;\;\;y=y(s)
\end{eqnarray}
の関数形を与えれば定まる。
$\;x,y\;$面を複素平面と考えて
\begin{eqnarray}
z=x+iy
\end{eqnarray}
とおけば
\begin{eqnarray}
z=z(s)
\end{eqnarray}
なる一つの複素関数を与えることによってヒゲの形を示すことが出来る。
$\;s\;$はヒゲの取り付け位置からの距離だから勿論実数である。
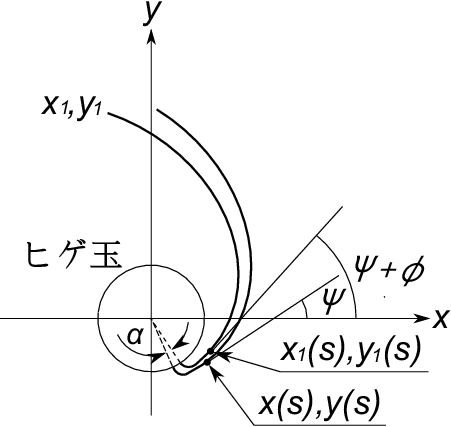
任意の1点$\;x(s),y(s)\;$においてヒゲの曲線に接線を引きこれが$\;x\;$軸となす角を$\;\Psi\;$とすれば
\begin{eqnarray}
\frac{dx}{ds}=cos\Psi\;\;\;\;\;\frac{dy}{ds}=sin\Psi
\end{eqnarray}
である。したがって複素表示を用いれば
\begin{eqnarray}
\frac{dz}{ds}=\frac{dx}{ds}+i\frac{dy}{ds}=cos\Psi+isin\Psi=e^{i\Psi}
\end{eqnarray}
のような関係が得られる(第5部 数学公式集 5-6 オイラーの公式参照)。
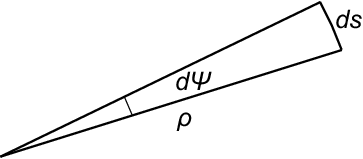
曲率半径$\;\rho\;$は下図を見ればわかるように$\;\Psi\;$を使って
天真がこの位置から$\;\alpha\;$だけ回転したときヒゲは図に示すように
\begin{eqnarray}
z_1(s)=x_1(s)+iy_1(s)
\end{eqnarray}
なる曲線で示される形に変わったとする。この曲線への接線が$\;x\;$軸となす角を
$\;\Psi + \phi\;$とすれば前と同様に
\begin{eqnarray}
\frac{dz_1}{ds}=e^{i(\Psi+\phi)}
\end{eqnarray}
が成立し、またこの曲線の$\;s\;$点における曲率半径$\;\rho_1\;$は
\begin{eqnarray}
\frac{1}{\rho_1}=\frac{d(\Psi+\phi)}{ds}
\end{eqnarray}
で与えられる。したがってヒゲ玉から$\;s\;$なる距離にあるヒゲの部分の曲率半径は$\;\rho\;$から$\;\rho_1\;$へ変わり曲率の変化は
\begin{eqnarray}
\frac{1}{\rho_1}-\frac{1}{\rho}=\frac{d\phi}{ds}
\end{eqnarray}
となる。