グラフ作成ソフトにはいろいろな種類があるがgnuplotはプログラムを書く手間はあるがデータから
グラフを描くのはもちろん関数を描かせたりデータをフィッティング(最小2乗法で近似)したり3Dグラフを
描かせたりすることが出来るなどその応用範囲は非常に広い。
数値微分や数値積分も慣れれば簡単に記述することが出来る。
またどんなに複雑な微分方程式であってもプログラムを記述してしまえば簡単に数値解のグラフを描くことが出来る。
gnuplotの良さはグラフ作成プログラム上で数値解析も同時に行なえることである。
微分方程式の数値解析は基本的に次のようなアルゴリズムで行われる。
先ず微分の定義から
\begin{eqnarray}
y'=f(x,y)=\lim_{h \to 0} \frac{y(x+h)-y(x)}{h}
\end{eqnarray}
が成り立つ。ここで$\;h\;$ が小さいときは
\begin{eqnarray}
f(x,y)\approx \frac{y(x+h)-y(x)}{h} \nonumber \\
y(x+h)\approx y(x)+hf(x,y)
\end{eqnarray}
$x,y$の初期値を$x_0,y_0$とし、
\begin{eqnarray}
x_1&=&x_0+h,x_2=x_1+h,\cdots \nonumber \\
y_1&=&y_0+hf(x_0,y_0),y_2=y_1+hf(x_1.y_1),\cdots \nonumber
\end{eqnarray}
のようにおけば
\begin{eqnarray}
x_{n+1}&=&x_n+h \\
y_{n+1}&=&y_n+hf(x_n,y_n)
\end{eqnarray}
のように書ける。数値解析ではこれをコンピュータを使って繰り返し計算してゆき、関数$\;y\;$の全体の形を近似するのである。
これをオイラーの方法という。
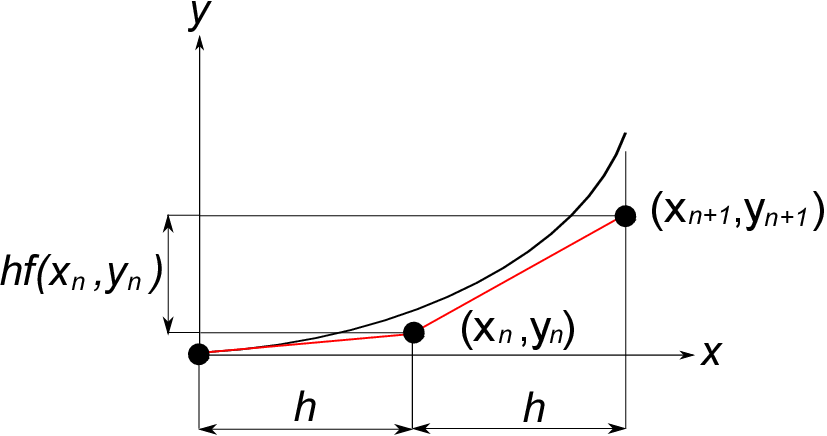
ここで$\;x\;$が$\;h\;$だけ増加したときの$\;y\;$の増分は$hf(x_n,y_n)$であるから、$f(x_n,y_n)$は関数$\;y\;$の局所的な傾きを表している。
$x_n,y_n$から$y_{n+1}$を予測するにはこの局所的な傾きを如何に精度良く求めるかが問題となる。
たとえば傾き$f(x_n,y_n)$を$\frac{1}{2}[f(x_n,y_n)+f(x_{n+1},y_n+hf(x_n,y_n))]$として近似の精度を高めたものをホインの方法という。
4次のルンゲクッタ法では傾きを4種類に分け更に重み付けをした上で次のように定める。
\begin{eqnarray}
y'&=&f(x,y), \;\;\;y(x_0)=y_0 \nonumber \\
y_{n+1}&=&y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4) \nonumber \\
k_1&=&f(x_n,y_n) \nonumber \\
k_2&=&f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1) \nonumber \\
k_3&=&f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2) \nonumber \\
k_4&=&f(x_n+h,y_n+hk_3)
\end{eqnarray}
このように微分方程式の数値解法にはいろいろな種類があるが、計算時間と精度の兼ね合いを考えると
4次のルンゲクッタ法が最も優れている。
計算精度は刻み幅$\;h\;$のおよそ4乗であり、例えば刻み幅$h=10^{-2}$だと精度は$10^{-8}$程度となる。
それでは4次のルンゲクッタ法を振り子の運動方程式を例にして試してみよう。
振り子の運動方程式は第1部 振り子の運動1-1より次式であった。
\begin{eqnarray}
ml\frac{d^2\theta}{dt^2}=-mgsin\theta
\end{eqnarray}
近似的な理論解を得るために第1部1-1では$sin\theta\approx\theta$とおいたが、数値解析ではその必要はない。
式(6)の両辺を$ml$で除すと
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta
\end{eqnarray}
これは2階微分方程式なので次のように連立1階微分方程式に直してやる。
\begin{eqnarray}
\frac{d\omega}{dt}&=&-\frac{g}{l}sin\theta \\
\frac{d\theta}{dt}&=&\omega
\end{eqnarray}
あとは式(5)に則って係数を逐次計算した上で$\theta_{n+1},\omega_{n+1}$を求めてゆくだけである。
ただしこの場合、連立微分方程式なので関数を$f(t,\theta,\omega)$と$g(t,\theta,\omega)$に分け、係数も$\;k\;$と$\;m\;$を使う。
連立といっても複雑に考える必要はなく、係数の式を同時並行的に計算していくことで勝手に連立方程式が解けてしまうのである。
どうするかというと、
\begin{eqnarray}
&\;&f(\theta,\omega,t)=\frac{d\omega}{dt}=-\frac{g}{l}sin\theta \nonumber \\
&\;&g(\theta,\omega,t)=\frac{d\theta}{dt}=\omega \nonumber \\
\end{eqnarray}
\begin{eqnarray}
&k_1&=f(\theta_n,\omega_n,t_n) \nonumber \\
&m_1&=g(\theta_n,\omega_n,t_n) \nonumber \\
&k_2&=f(\theta_n+0.5m_1,\omega_n+0.5k_1,t_n+0.5h) \nonumber \\
&m_2&=g(\theta_n+0.5m_1,\omega_n+0.5k_1,t_n+0.5h) \nonumber \\
&k_3&=f(\theta_n+0.5m_2,\omega_n+0.5k_2,t_n+0.5h) \nonumber \\
&m_3&=g(\theta_n+0.5m_2,\omega_n+0.5k_2,t_n+0.5h) \nonumber \\
&k_4&=f(\theta_n+m_3,\omega_n+k_3,t_n+h) \nonumber \\
&m_4&=g(\theta_n+m_3,\omega_n+k_3,t_n+h) \nonumber
\end{eqnarray}
\begin{eqnarray}
&\theta_{n+1}&=\theta_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4) \nonumber \\
&\omega_{n+1}&=\omega_n+\frac{h}{6}(m_1+2m_2+2m_3+m_4) \nonumber
\end{eqnarray}
のようにプログラムを記述して逐次計算すればよい。4-2のサンプルプログラムで実行例をみてみよう。