When considering the problem of the maximum & minimum value of the function, $f(x)$, one of the methods is to differentiate the function, $f(x)$ with respect to ''$x$'', and to find ''$x$'' which the
derived function, $df(x)/dx = 0$. In terms of ''$x$'' which the derived function becomes ''0'', the function, $f(x)$ becomes one of the maximum, minimum or inflection value. This is a basic term of the differential calculus.
As one of the quite similar math problems, it is what is called as the calculus of variations to consider the problem of the maximum & minimum values of the $G(x, y, y')$, (i.e. function of the functional shape which is called as ''functionals'') which is specified by the shape of the function, $f(x)$.
In terms of the functional shape which makes the minimal variation ''0'', the functionals take one of the maximum, minimum or stationary value. What we want to obtain is the functional shape, $f(x)$ like this. In other words, when the functionals take the maximum or minimum value, it becomes ''$\delta G = 0$''. The calculus of variations are regarded like differentiating the function with respect to the function, so to speak.
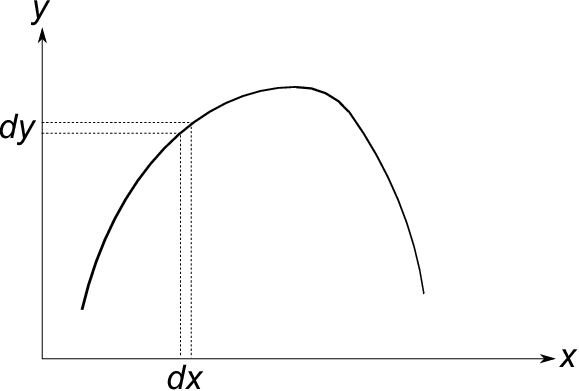
The figure below shows the image of the differential calculus. As the variable, ''$x$'' is changed a little, the value of the function, $f(x)$ is correspondingly changed a little, but the shape itself of the curved line remains unchanged.
In case of the variational problem, the figure below shows its image. When the variable, ''$x$'' is changed a little, what is changed is not the value of the function, $f(x)$, but the shape of the function, $f(x)$ as shown in the figure below.

In order to figure out the calculus variations, the Euler-Lagrange equation has to be figured out. When the functionals , ''$G$'' are defined as the integration of the function, $f(x, y, y')$ such as ''$G\{x,y,y'\}=\int_a^bf(x,y,y')dx$'', $f(x, y, y')$ which gives the functionals the maximum & minimum values can be obtained by figuring out the Euler-Lagrange equation.
Note that when the functionals are described as ''$f (x, y, y')$'', if that notation seems to be complicated, the notation of ''$f [y]$'' instead of ''$f (x, y, y')$'' will be used in this book to avoid any confusion.
Now, assuming that we have the function, ''$y = y(x)$'', and the function, ''$f$'' which is determined by $x$, $y$, $y'$. The functionals, ''$G$'' is given in the integral form by the integration of this ''$f$'' as shown in the equation (1).
\begin{eqnarray}
G[y]=\int_a^bf(x,y,y')dx
\end{eqnarray}
The variational problem is to obtain the functional shape of the function, ''$f$'', so that this ''$G$'' has the maximum & minimum values. The basic perspective is the same as the differentiation, utilizing that when the functional shape is changed a little at the vicinity of the maximum & minimum values, the variations of the functionals, ''$\delta G$'' (called as the first variation) are very little.
Assuming that the function, ''$y(x)$'' was the function, ''$y_0 (x)$'' at first, in terms of this, introducing the arbitrary function, ''$H(x)$'' & very small certain amount ''$\xi$'', we will try to transform $y(x)$ just a little as shown in the following equation (2). The initial condition such as the equation (3) is given to the ''$H(x)$'' so that no distortion can be assured at the both ends of the interval of the integration.
\begin{eqnarray}
y(x)&=&y_0(x)+\xi H(x) \\
\frac{\partial y}{\partial \xi}&=&H(x) \nonumber \\
\frac{\partial y'}{\partial \xi}&=&H'(x) \nonumber \\
H(a)&=&H(b)=0
\end{eqnarray}
The ''$\xi$'' above is the variable to let the functional shape transform, and in terms of the functional shape which gives the functionals, ''$G[y]$'' the maximum & minimum values, the transformation of the functionals should be very small, even if the functional shape transformes just a little. Accordingly, the condition that ''$f (x)$'' gives the maximum & minimum values can be proven with the following equation (4).
\begin{eqnarray}
\{\frac{dG[y]}{d\varepsilon}\}_{\varepsilon=0}=0
\end{eqnarray}
Then, differentiating the functionals of the equation (1) with respect to ''$\xi$'', and using the formula (refer to the Section 5 Mathematical Formulas 5-2-4) of the integration by parts, the equation (5) can be obtained.
\begin{eqnarray}
\frac{dG}{d\xi}&=&\frac{d}{d\xi}\int_a^bf(x,y,y')dx \nonumber \\
&=&\int_a^b(\frac{\partial f}{\partial y}\frac{\partial y}{\partial \xi}+\frac{\partial f}{\partial y'}\frac{\partial y'}{\partial \xi})dx \nonumber \\
&=&\int_a^b\{\frac{\partial f}{\partial y}H(x)+\frac{\partial f}{\partial y'}H'(x)\}dx \nonumber \\
&=&[\frac {\partial f}{\partial y'}H(x)]_a^b+\int_a^bH(x)\{\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})\}dx \nonumber \\
&=&\int_a^bH(x)\{\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})\}dx
\end{eqnarray}
$[\frac {\partial f}{\partial y'}H(x)]_a^b$ of the 4th line becomes ''0'' according to the initial condition.
Here, as ''$H(x)$'' is the arbitrary function, the part of the ''$\{ \}$'' needs to be ''0 (zero)'' in order for the right side of the equation to identically become ''0 (zero)''. Based on this, in order for the functionals, ''$G$'' to take the maximum & minimum values, the equation (6) is needed.
\begin{eqnarray}
\frac{dG}{d\xi}=\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})=0
\end{eqnarray}
In other words, the equation (7) comes from the equation (6).
\begin{eqnarray}
\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})=0
\end{eqnarray}
Assuming that ''$\frac{\partial f}{\partial y}=f_y,\; \frac{\partial f}{\partial y'}=f_z,\;f=f(x,y,y')=f[y(x)]$'' , the equation (8) can be obtained.
\begin{eqnarray}
\frac{d}{dx}f_z[y(x)]=f_y[y(x)]
\end{eqnarray}
This is called as ''Euler-Lagrange equation'' or simply ''Euler equation''.