1-1で求めた振り子の運動方程式の解は$\;cos\;$の形をしているが、
初期条件を変えてやるとこれを$\;sin\;$の形にすることが出来る。
振り子の運動方程式は
\begin{eqnarray}
\frac{d^2\theta}{dt^2}=-\frac{g}{l} \theta
\end{eqnarray}
であった。
$\;sin\;$の形の解を求める為にラプラス変換するときの初期条件を次のように変えてみよう。
\[\theta_{t=0}=0\;\;\;\;\;\;\;\;(\frac{d\theta}{dt})_{t=0}=\omega_0\]
とおいて式(1)をラプラス変換(第5部 数学公式集 ラプラス変換表5-3-2参照)すれば
\begin{eqnarray}
&\;&s^2\Theta(s)-s\theta_{t=0}-(\frac{d\theta}{dt})_{t=0}=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&s^2\Theta(s)-\omega_0=-\frac{g}{l}\Theta(s) \nonumber \\
&\;&(s^2+\frac{g}{l})\Theta(s)=\omega_0 \nonumber \\
&\;&\Theta(s)=\frac{\omega_0}{(s^2+\frac{g}{l})}
\end{eqnarray}
ラプラス逆変換(第5部 数学公式集 ラプラス変換表5-3-2参照)すると
\begin{eqnarray}
\theta=\omega_0\sqrt{\frac{l}{g}}\;sin\sqrt{\frac{g}{l}} t=\frac{\omega_0}{\omega_n}\;sin\;\omega_n t
\end{eqnarray}
これをグラフで表すと図のようになる。ただし、角速度の初速$\;\omega_0\;$は1-2で求めた$\;\omega_{max}\;$の値$=0.313\;[rad/s]$とした。
こうすれば当たり前だが$\;cos\;$のときと同じ振り角となる。
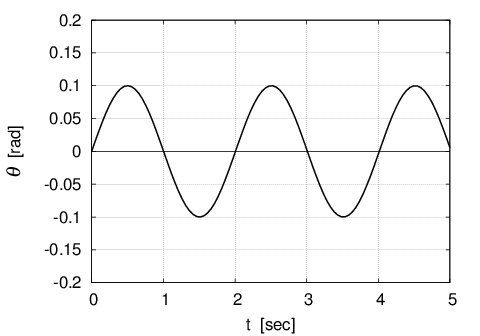
これは振り子が鉛直真下にあるときに右方向に角速度の初速$\;\omega_0\;$を与えた瞬間を時刻0としたとき、その後の時刻における振り子の運動の様子を表している。