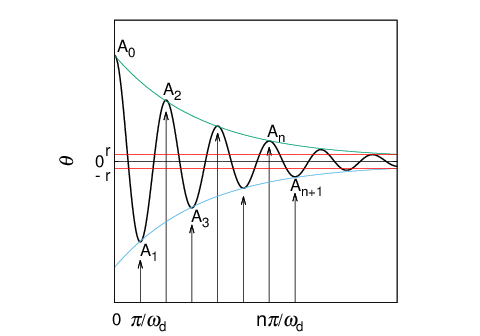
2-3からテンプの運動方程式の解は
\begin{eqnarray}
\theta\pm r=(A_0\pm r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
と表せるのであった。
角速度は式(1)を$\;t\;$で微分すれば
\begin{eqnarray}
\frac{d\theta}{dt}&=&-\frac{(A_0\pm r)}{\sqrt{1-\zeta^2}}\{\zeta\omega_n e^{-\zeta\omega_n t}cos(\omega_d t-\phi)+\omega_d\;e^{-\zeta\omega_n t}sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{(A_0\pm r)}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\omega_n\{\zeta\; cos(\omega_d t-\phi)+\sqrt{1-\zeta^2}\;sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{(A_0\pm r)}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\;\omega_n\;sin\omega_d t
\end{eqnarray}
これより式(1)は振り子のときと同じように周期$\;2\pi/\omega_d\;$の周期を持つことがわかる。
次に固体摩擦があるときのテンプの自由振動の極大極小値を求めてみよう。
今、$\;t=0\;$で$\;\theta\;$が正の極大値をとったとする。$\;t=0\;$では$\;\frac{d\theta}{dt}=0\;$であり、$\;t>0\;$の最初の1振動では
$\;\frac{d\theta}{dt}<0\;$であるから復号はーをとる。
\begin{eqnarray}
\theta=(A_0-r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}\;cos(\omega_d t-\phi)+r
\end{eqnarray}
1回目の極小値$\;|A_1|\;$は式(3)に\[t=\frac{\pi}{\omega_d}\]を代入して
\begin{eqnarray}
A_1&=&(A_0-r)\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos(\pi-\phi)+r \nonumber \\
&=&-(A_0-r)\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos\phi+r \nonumber \\
&=&-(A_0-r)e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}+r \\
|A_1|&=&(|A_0|-r)e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}-r
\end{eqnarray}
ここで粘性減衰だけが作用した場合の1振動毎の減衰比
\begin{eqnarray}
\lambda=e^{\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
を用いると式(5)は次のようになる。
\begin{eqnarray}
|A_1|=\frac{1}{\lambda}(|A_0|-r)-r
\end{eqnarray}
これより
\begin{eqnarray}
|A_0|-|A_1|=(1-\frac{1}{\lambda})|A_0|+r\frac{1+\lambda}{1-\mu}(\frac{1}{\lambda}-1)
\end{eqnarray}
同様に2回目の正の極大値$\;|A_2|\;$は式(1)の復号に注意して
\begin{eqnarray}
\theta=(A_1+r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}\;cos(\omega_d t-\phi)-r
\end{eqnarray}
$\;A_1\;$のときと同様に\[t=\frac{\pi}{\omega_d}\]として
\begin{eqnarray}
A_2&=&(A_1+r)\frac{e^{-\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}cos(\pi-\phi)-r \nonumber \\
&=&-(A_1+r)\frac{e^{-\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}cos(\phi)-r \nonumber \\
&=&-(A_1+r)e^{-\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}-r
\end{eqnarray}
\begin{eqnarray}
|A_2|&=&\frac{1}{\lambda}(|A_1|-r)-r \nonumber \\
&=&\frac{1}{\lambda}[\{\frac{1}{\lambda}(|A_0|-r)-r\}-r]-r \nonumber \\
&=&\frac{1}{\lambda^2}|A_0|-r(\frac{1}{\lambda^2}+\frac{2}{\lambda}+1)
\end{eqnarray}
\begin{eqnarray}
|A_0|-|A_2|=(1-\frac{1}{\lambda^2})|A_0|+r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda^2}-1) \nonumber \\
\end{eqnarray}
また
\begin{eqnarray}
|A_1|-|A_2|=(1-\frac{1}{\lambda})|A_1|+r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda}-1)
\end{eqnarray}
となる。
同様に$\;N\;$回目の極大値$\;|A_N|\;$とそれから$\;n\;$振動後の振り角$\;|A_{N+n}|\;$との関係を求めると
\begin{eqnarray}
\Delta A_n=|A_N|-|A_{N+n}|=a|A_N|+b
\end{eqnarray}
ただし
\begin{eqnarray}
a&=&1-\frac{1}{\lambda^n} \\
b&=&r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda^n}-1)
\end{eqnarray}
振動の1周期あたりの振り角損失$\;\Delta A\;$は式(13)で$\;A_N=A,n=2\;$とおいて
\begin{eqnarray}
\Delta A&=&(1-\frac{1}{\lambda^2})A+r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda^2}-1) \nonumber \\
&=&(1-\frac{1}{\lambda^2})(A-r\frac{1+\lambda}{1-\lambda}) \nonumber \\
&=&(1-e^{-\frac{2\;\zeta\;\pi}{\sqrt{1-\zeta^2}}})(A-r\frac{1+e^{\frac{\zeta \;\pi}{\sqrt{1-\zeta^2}}}}{1-e^{\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}}) \nonumber \\
&\approx&\frac{2\;\zeta\;\pi}{\sqrt{1-\zeta^2}}(A+r\frac{2+\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}{\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&=&\frac{2\zeta\;\pi}{\sqrt{1-\zeta^2}}(A+r\frac{2\sqrt{1-\zeta^2}+\zeta\;\pi}{\zeta\;\pi}) \nonumber \\
&=&\frac{2\zeta\;\pi}{\sqrt{1-\zeta^2}}(A+r)+4r \nonumber \\
&=&\zeta\;\omega_n\;T_d(A+r)+4r\;\;\;\;\;\;(\because T_d=\frac{2\pi}{\omega_d}=\frac{2\pi}{\sqrt{1-\zeta^2}\;\omega_n}) \\
&\approx&\frac{c}{2I}T_dA+4r\;\;\;\;\;\;(\because \zeta \omega_n=\frac{c}{2\sqrt{Ik}}\sqrt{\frac{k}{I}}=\frac{c}{2I}\;\;\;\;\;\; cr\ll1)\;\;\;\;\;\;\;\;\;\;
\end{eqnarray}
ここで
\begin{eqnarray}
\mu=\frac{c}{2I}
\end{eqnarray}
とおくと式(17)は次のように表される。
\begin{eqnarray}
\Delta A=\mu T_dA+4r
\end{eqnarray}
ただし$\;T_d\;$は減衰があるときのテンプの周期で次式で表される。
\begin{eqnarray}
T_d=\frac{2\pi}{\omega_d}=\frac{2\pi}{\sqrt{1-\zeta^2}\omega_n}=\frac{2\pi}{\sqrt{1-\zeta^2}}\sqrt{\frac{I}{k}}
\end{eqnarray}
ここで振り子のときと同じように$\;Q\;$値を求めてみよう。
まずテンプの保有エネルギー$\;E\;$を求めてみる。図のようにバネ定数$\;k\;$のヒゲゼンマイがその内端を
角度$A$だけ移動されたときの復元トルク$\;T\;$は$\;-kA\;$である。
トルクの次元は力×距離だからトルク自体がエネルギーを表す。
テンプの保有エネルギーはトルク$\;kA\;$を$\;\Delta A\;$毎に0〜$\;A\;$まで寄せ集めた(積分した)ものだから
下図の三角形の面積がテンプの保有エネルギーとなる。
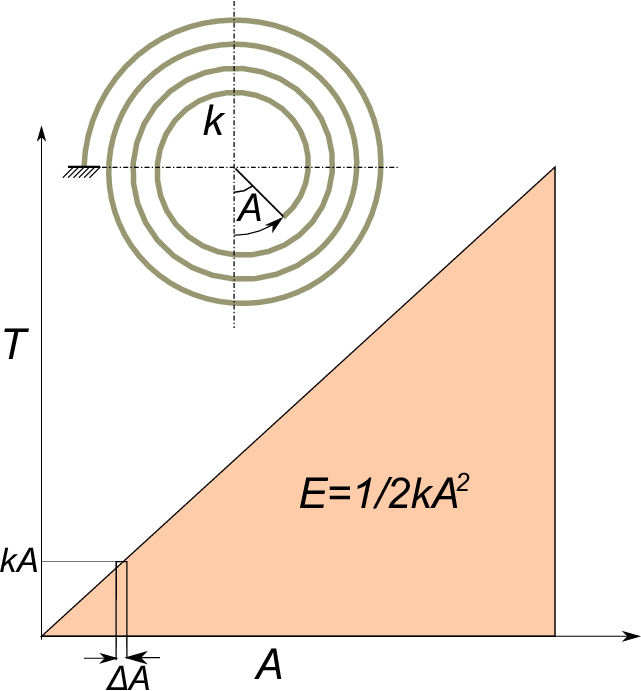
したがって
\begin{eqnarray}
E=\frac{1}{2}kA^2
\end{eqnarray}
式(21)を$\;A\;$で微分すると
\begin{eqnarray}
\Delta E=kA\Delta A
\end{eqnarray}
式(22)に式(19)を代入すると
\begin{eqnarray}
\Delta E=kA\{\mu T_dA+4r\}
\end{eqnarray}
Q値の定義式$\;Q=2\pi\frac{E}{\Delta E}\;$に式(21)と式(23)を代入すると
\begin{eqnarray}
Q&=&2\pi\frac{E}{\Delta E} \nonumber \\
&=&\frac{\pi\;A}{\mu T_dA+4r} \nonumber \\
&=&\frac{\pi}{\mu T_d+4r/A}
\end{eqnarray}
式(24)で$\;r=0\;$の場合は
\begin{eqnarray}
Q&=&\frac{\pi}{\mu T_d} \nonumber \\
&=&\frac{2I\pi}{cT_d} \nonumber \\
&=&\frac{\pi\;I\;f}{c} \\
&=&\frac{\sqrt{1-\zeta^2}}{2\zeta}
&\approx&\frac{1}{2\zeta}\;\;\;\;\;\;\;\;\;\;\;(\zeta \ll1)
\end{eqnarray}
となり第1部1-5 振り子の$\;Q\;$値と一致する。
ここで
$\;I\;$:テンワの慣性モーメント
$\;c\;$:粘性減衰係数
$\;f\;$:振動数
である。
テンプを自由振動させたとき振り子のときと同じように振り角が半減するまでの時間を$\;t_1\;$とすれば
\[
0.5=e^{-\zeta \omega_n t_1}=exp\{-\frac{c\; t_1}{2I}\} \nonumber \\
\]
とおいて両辺の対数をとれば
\begin{eqnarray}
\ln{0.5}&=&-\frac{c\; t_1}{2I} \nonumber \\
&=&-\frac{\pi f t_1}{2Q} \nonumber
\end{eqnarray}
これより振り子のときと同じように$\;t_1\;$を実測すると$\;c\;$や$\;\zeta\;$が求まり、$\;Q\;$値を次式で計算することが出来る。
\begin{eqnarray}
Q=-\frac{\pi f t_1}{2\ln{0.5}}=2.26618\;f\;t_1
\end{eqnarray}
尚、一般的な腕時計の$\;Q\;$値は150〜400程度が普通である。