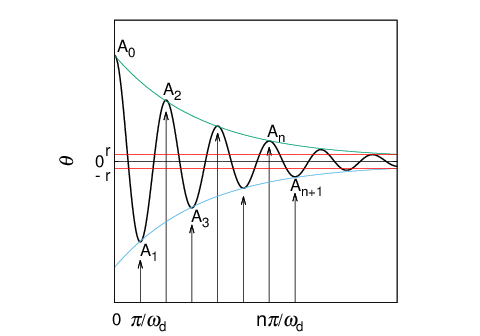
The solution of equation of motion of balance is represented the equation (1) as in clause 2-3.
\begin{eqnarray}
\theta\pm r=(A_0\pm r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} cos(\omega_d t-\phi)
\end{eqnarray}
The angular velocity can be indicated by differentiating the equation (1) with respect to ''$t$'' as shown in the equation (2).
\begin{eqnarray}
\frac{d\theta}{dt}&=&-\frac{(A_0\pm r)}{\sqrt{1-\zeta^2}}\{\zeta\omega_n e^{-\zeta\omega_n t}cos(\omega_d t-\phi)+\omega_d\;e^{-\zeta\omega_n t}sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{(A_0\pm r)}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\omega_n\{\zeta\; cos(\omega_d t-\phi)+\sqrt{1-\zeta^2}\;sin(\omega_d t-\phi)\} \nonumber \\
&=&-\frac{(A_0\pm r)}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\;\omega_n\;sin\omega_d t
\end{eqnarray}
Accordingly, it can be figured out that the equation (1) has the period of ''$2\pi/\omega_d$'' which is the same as that of the pendulum.
Next we find the maximum & minimum values of the displacement during the free vibration of the balance when the solid friction works. Assuming that ''$\theta$'' represents the plus
maximum value at ''$t = 0$''.
At ''$t = 0$'', ''$d\theta/dt$'' becomes ''0'' (''$d\theta/dt = 0$''), and at the first one oscillation of the ''$t>0$''
condition, it becomes ''$d\theta/dt<0$''. Accordingly, the plus-minus notation is ''-'' in this case.
\begin{eqnarray}
\theta=(A_0-r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}\;cos(\omega_d t-\phi)+r
\end{eqnarray}
In terms of the first minimum value,''$A_1$''can be firstly obtained by substituting ''$t = \pi/\omega_d$'' to the equation (3) as shown in the equation (4). Then, ''$|A_1|$'' can be obtained as shown in the equation (5).
\begin{eqnarray}
A_1&=&(A_0-r)\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos(\pi-\phi)+r \nonumber \\
&=&-(A_0-r)\frac{e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}\;cos\phi+r \nonumber \\
&=&-(A_0-r)e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}+r \\
|A_1|&=&(|A_0|-r)e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}-r
\end{eqnarray}
In case that only the viscous damping works, when the one vibration by one vibration damping ratio which is represented as the equation (6) is used, the equation (5) becomes the equation (7).
\begin{eqnarray}
\lambda=e^{\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}
\end{eqnarray}
\begin{eqnarray}
|A_1|=\frac{1}{\lambda}(|A_0|-r)-r
\end{eqnarray}
Furthermore, the equation (8) can be obtained from the equation (7)
\begin{eqnarray}
|A_0|-|A_1|=(1-\frac{1}{\lambda})|A_0|+r\frac{1+\lambda}{1-\mu}(\frac{1}{\lambda}-1)
\end{eqnarray}
In the same way, in terms of the second plus maximum value,''$A2$'' can be firstly indicated by substituting ''$t = \pi/ \omega_d$'' to the equation (9), paying attention to the plus-minus notation of the equation (1) as obtained in the equation (10). Then, ''$|A2|$'' can be obtained as shown in the equation (11).
\begin{eqnarray}
\theta=(A_1+r)\frac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}}\;cos(\omega_d t-\phi)-r
\end{eqnarray}
\begin{eqnarray}
A_2&=&(A_1+r)\frac{e^{-\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}cos(\pi-\phi)-r \nonumber \\
&=&-(A_1+r)\frac{e^{-\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}}{\sqrt{1-\zeta^2}}cos(\phi)-r \nonumber \\
&=&-(A_1+r)e^{-\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}-r
\end{eqnarray}
\begin{eqnarray}
|A_2|&=&\frac{1}{\lambda}(|A_1|-r)-r \nonumber \\
&=&\frac{1}{\lambda}[\{\frac{1}{\lambda}(|A_0|-r)-r\}-r]-r \nonumber \\
&=&\frac{1}{\lambda^2}|A_0|-r(\frac{1}{\lambda^2}+\frac{2}{\lambda}+1)
\end{eqnarray}
Then, the equations (12) & (13) can be obtained.
\begin{eqnarray}
|A_0|-|A_2|=(1-\frac{1}{\lambda^2})|A_0|+r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda^2}-1)
\end{eqnarray}
\begin{eqnarray}
|A_1|-|A_2|=(1-\frac{1}{\lambda})|A_1|+r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda}-1)
\end{eqnarray}
Clarifying the relationship of the displacement between the ''$N$''th maximum value, ''$A_N$'' and ''$n$'' vibrations after that, ''$A_{N+n}$'', the equation (14) can be obtained assuming that ''$a$'' and ''$b$'' are defined as the equations (15) & (16) respectively.
\begin{eqnarray}
\Delta A_n=|A_N|-|A_{N+n}|=a|A_N|+b
\end{eqnarray}
\begin{eqnarray}
a&=&1-\frac{1}{\lambda^n} \\
b&=&r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda^n}-1)
\end{eqnarray}
The displacement loss, $\Delta A$ in every period of the oscillation can be obtained in the equation (18) assuming that ''$A_N=A$'' & ''$n=2$'' of the equation (14).
\begin{eqnarray}
\Delta A&=&(1-\frac{1}{\lambda^2})A+r\frac{1+\lambda}{1-\lambda}(\frac{1}{\lambda^2}-1) \nonumber \\
&=&(1-\frac{1}{\lambda^2})(A-r\frac{1+\lambda}{1-\lambda}) \nonumber \\
&=&(1-e^{-\frac{2\;\zeta\;\pi}{\sqrt{1-\zeta^2}}})(A-r\frac{1+e^{\frac{\zeta \;\pi}{\sqrt{1-\zeta^2}}}}{1-e^{\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}}) \nonumber \\
&\approx&\frac{2\;\zeta\;\pi}{\sqrt{1-\zeta^2}}(A+r\frac{2+\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}{\frac{\zeta\;\pi}{\sqrt{1-\zeta^2}}}) \nonumber \\
&=&\frac{2\zeta\;\pi}{\sqrt{1-\zeta^2}}(A+r\frac{2\sqrt{1-\zeta^2}+\zeta\;\pi}{\zeta\;\pi}) \nonumber \\
&=&\frac{2\zeta\;\pi}{\sqrt{1-\zeta^2}}(A+r)+4r \nonumber \\
&=&\zeta\;\omega_n\;T_d(A+r)+4r\;\;\;\;\;\;(\because T_d=\frac{2\pi}{\omega_d}=\frac{2\pi}{\sqrt{1-\zeta^2}\;\omega_n}) \\
&\approx&\frac{c}{2I}T_dA+4r\;\;\;\;\;\;(\because \zeta \omega_n=\frac{c}{2\sqrt{Ik}}\sqrt{\frac{k}{I}}=\frac{c}{2I}\;\;\;\;\;\; cr\ll1)\;\;\;\;\;\;\;\;\;\;
\end{eqnarray}
Here, on the assumption of the equation (19), the equation (18) can be represented as shown in the equation (20).
\begin{eqnarray}
\mu=\frac{c}{2I}
\end{eqnarray}
\begin{eqnarray}
\Delta A=\mu T_dA+4r
\end{eqnarray}
Note that ''$T_d$'' is the period of the balance when the damping works, and ''$T_d$'' can be represented by the equation (21).
\begin{eqnarray}
T_d=\frac{2\pi}{\omega_d}=\frac{2\pi}{\sqrt{1-\zeta^2}\omega_n}=\frac{2\pi}{\sqrt{1-\zeta^2}}\sqrt{\frac{I}{k}}
\end{eqnarray}
We find the Quality factor of the balance here as well as the case of the pendulum.
Firstly, we will find the retaining energy of the balance, ''$E$''. As shown in the figure below, when the hairspring whose spring constant, ''$k$'' travels the inner end to the ''$A$'' angles, the restoring torque, ''$T$'' is ''$-kA$''
As the dimension of the torque is ''Force x (multiplied by) Distance'', the torque itself represents the energy. Due to the fact that the retaining energy of the balance is what the torque, ''$kA$'' are gathered in $\Delta A$ by $\Delta A$ from ''0'' to ''$A$'' ( in other words, integrated), which means that the triangle area of the figure below represents the retaining energy of the balance.
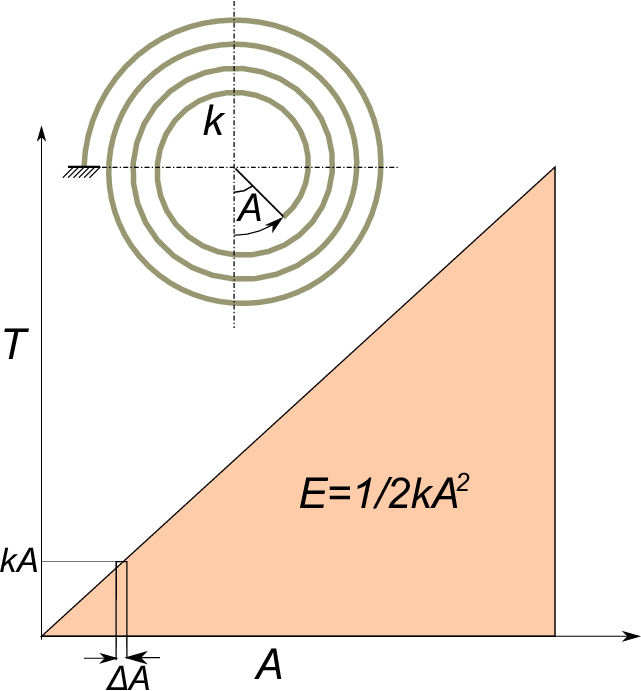
Accordingly, the retaining energy of the balance, ''$E$'' is shown in the equation (22).
\begin{eqnarray}
E=\frac{1}{2}kA^2
\end{eqnarray}
Differentiating the equation (22) with respect to ''A'', the equation (23) can be obtained.
\begin{eqnarray}
\Delta E=kA\Delta A
\end{eqnarray}
Substituting the equation (20) to the equation (23), the equation (24) can be obtained.
\begin{eqnarray}
\Delta E=kA\{\mu T_dA+4r\}
\end{eqnarray}
Substituting the equations (22) & (24) to the equation (1) in clause 1-5, the equation (25) can be obtained.
\begin{eqnarray}
Q&=&2\pi\frac{E}{\Delta E} \nonumber \\
&=&\frac{\pi\;A}{\mu T_dA+4r} \nonumber \\
&=&\frac{\pi}{\mu T_d+4r/A}
\end{eqnarray}
In case of ''$r = 0$'' in the equation (25), the equation (26) can be obtained.
The equation (26) can be further converted to the following two equations below which entirely correspond to the equations (11) & (12) obtained previously in clause 1-5.
\begin{eqnarray}
Q&=&\frac{\pi}{\mu T_d} \nonumber \\
&=&\frac{2I\pi}{cT_d} \nonumber \\
&=&\frac{\pi\;I\;f}{c} \\
&=&\frac{\sqrt{1-\zeta^2}}{2\zeta}
&\approx&\frac{1}{2\zeta}\;\;\;\;\;\;\;\;\;\;\;(\zeta \ll1)
\end{eqnarray}
Conditions:
$\;I\;$:Moment of inertia of the balance wheel
$\;c\;$:Viscous damping coefficient
$\;f\;$:Frequency (Be noted that ''$f$'' of the equation (26) is the watch frequency which means 2 times of general frequency.)
When the balance is doing the free vibration, in terms of the ''$t_1$'' for the time for reducing the amplitude by half as well as the case of the pendulum, the following equation can be introduced.
\[
0.5=e^{-\zeta \omega_n t_1}=exp\{-\frac{c\; t_1}{2I}\} \nonumber \\
\]
Then, the same equation (13) in clause 1-5 can be also obtained by taking the logarithm of both sides of this equation.
\begin{eqnarray}
\ln{0.5}&=&-\frac{c\; t_1}{2I} \nonumber \\
&=&-\frac{\pi f t_1}{2Q} \nonumber
\end{eqnarray}
Accordingly, parameters ''$c$'' and ''$\zeta$'' can be obtained by actually measuring ''$t_1$'', and
the Quality factor can be calculated by the following equation (28).
\begin{eqnarray}
Q=-\frac{\pi f t_1}{2\ln{0.5}}=2.26618\;f\;t_1
\end{eqnarray}
The Quality factor of general wrist watch is normally approx. 150〜400.