3-3 ヒゲゼンマイ一般理論

3-3-3 ヒゲの弾性エネルギー

物体に外力が作用すると、その物体を構成する要素は外力の種類、大きさ、方向などによって

決まるある方向に移動する。すなわち物体は変形する。

したがって物体に外力が作用すると仕事がなされ、その仕事は弾性的に位置のエネルギーとして貯えられる。

このように貯えられた位置のエネルギーは外力が取り去られると外部に吐き出される。

このように物体に貯えられる位置のエネルギーを弾性エネルギーと呼ぶ。

長さ$\;L\;$の物体を力$\;P\;$で引っ張ったとき物体の断面には応力$\;\sigma\;$が発生しひずみ$\;\varepsilon\;$が生ずる。

このときの応力$\;\sigma\;$とひずみ$\;\varepsilon\;$の関係はフックの法則から

$$\begin{eqnarray} \sigma=E\varepsilon \end{eqnarray}$$

で表される。

物体の断面積を$\;A\;$とすると$\;P=A\sigma\;$であるから、物体の伸び$\;\lambda\;$は

$$\begin{eqnarray} \lambda&=&\varepsilon L=\frac{\sigma L}{E}=\frac{L}{AE}P \\ P&=&\frac{AE}{L}\lambda \end{eqnarray}$$

となる。

したがって弾性エネルギー$\;U\;$はバネの保有エネルギー$\;E=1/2kx^2\;$の

バネ定数$\;k\;$を$\;AE/L\;$に置き換えたものに等しいから

$$\begin{eqnarray} U=\frac{AE}{2L}\lambda^2 \end{eqnarray}$$

となる。式(2)を式(4)に代入すると

$$\begin{eqnarray} U=\frac{\sigma^2}{2E}AL \end{eqnarray}$$

と表すことが出来る。

次に図に示すように曲げモーメント$\;M\;$を受けるヒゲゼンマイの内部には曲げ応力$\;\sigma\;$を生じ、

これによる弾性エネルギー$\;U\;$は微小体積$\;dV=dAdx\;$に貯えられる引張または圧縮応力による

弾性エネルギーをヒゲゼンマイの全断面および全長にわたって積分したものになる。

すなわち

$$\begin{eqnarray} U=\int dU=\int \frac{\sigma^2}{2E}dV=\int \int \frac{\sigma^2}{2E}dA\;dx \end{eqnarray}$$

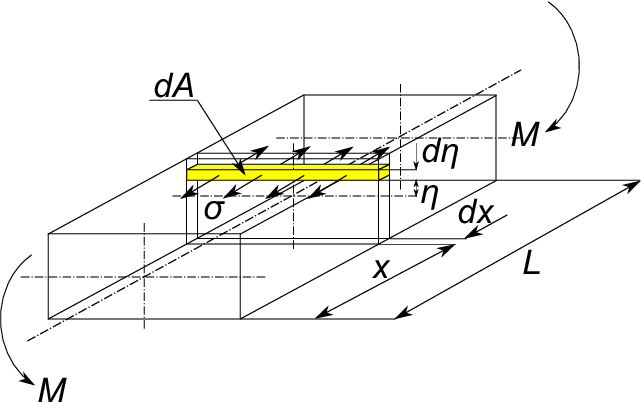
3-3-1より曲げ応力$\;\sigma\;$は $$\begin{eqnarray} \sigma=E\varepsilon=E\frac{\eta}{\rho} \end{eqnarray}$$

曲率半径$\;\rho\;$はヒゲゼンマイの断面2次モーメントを$\;I_H\;$とすれば

$$\begin{eqnarray} \frac{1}{\rho}=\frac{M}{EI_H} \end{eqnarray}$$

であるから式(8)を式(7)に代入すれば

$$\begin{eqnarray} \sigma=\frac{M}{I_H}\eta \end{eqnarray}$$

である。式(9)を式(6)に代入すると

$$\begin{eqnarray} U=\int \frac{M^2}{2EI_H^2}ds\int_A\eta^2dA&=&\int_0^L\frac{M^2}{2EI_H}ds \\ \because \int_A\eta^2dA&=&I_H \nonumber \end{eqnarray}$$

となる。一方、ヒゲを角度$\;\phi\;$だけ変形させたときのモーメント$\;M\;$は3-3-1から

$$\begin{eqnarray} M=EI_H\frac{d\phi}{ds} \end{eqnarray}$$

である。式(11)を式(10)に代入し、3-3-1から$\;k=EI_H/L\;$の関係を用いると

ヒゲの貯える弾性エネルギー$\;U\;$は

$$\begin{eqnarray} U=\frac{kL}{2}\int_0^L(\frac{d\phi}{ds})^2ds \end{eqnarray}$$

となる。

• トップページへ戻る
• このページの先頭へ

---

Copyright (C) 2014- 笹谷　卓史 All Rights Reserved.