旋盤を使って軸を作る場合は必ず軸振れ$\;e_{p-p}\;$が発生する。これは旋盤の回転中心がわずかに振れ回っているために生ずる。
この結果天真ほぞは図のように本来の回転中心(テンプの重心位置)から$\;e/2\;$だけ離れたところに実際の回転中心がきて
等時性を乱す原因となる。
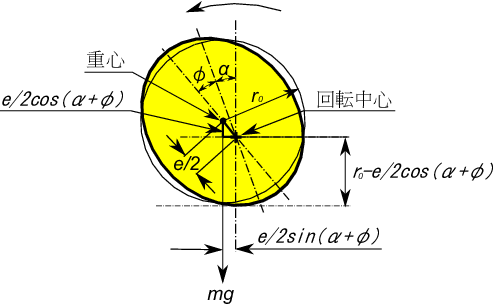
この場合の天真ほぞ半径(実際の回転中心と軸穴接地点との距離)は次のように表される。
\begin{eqnarray}
r=r_0-\frac{e}{2}cos(\alpha+\phi)
\end{eqnarray}
ここで
$\;r_0\;:\;$天真の平均半径、$e\;:\;$振れ量($\;p-p\;$値)、$\;\alpha\;:\;$天真の回転角、
$\;\phi\;:\;$テンプ中立点での振れ最大値方向と垂直軸とのなす角である。
そうするとテンプの中立点($\;\theta=0\;$)におけるテンプの自重による回転モーメント$\;M\;$は
\begin{eqnarray}
M=mgx=mg\frac{e}{2}sin\phi
\end{eqnarray}
となりここから$\;\alpha\;$だけテンプが回転したときの回転モーメントは
\begin{eqnarray}
M=mgx=mg\frac{e}{2}sin(\alpha+\phi)
\end{eqnarray}
となる。これよりテンプの運動方程式は次のようになる。
\begin{eqnarray}
I\frac{d^2 \theta}{dt^2}=\frac{mge}{2}sin(\alpha+\phi)-k\theta
\end{eqnarray}
ここで
$\;I\;$:テンワの慣性モーメント,$\;m\;$:テンプ質量,$\;g\;$:重力加速度,$\;\theta\;$:テンプ回転角度とする。
等時性誤差は3-1で外乱トルク$\;f(\theta)\;$が式(4)の右辺第1項だから次のようになる。
尚、式の変形には三角関数の加法定理(第5部 数学公式集 5-1-4)を使っている。
\begin{eqnarray}
\delta&=&-\frac{1}{A^2kT}\int_0^T\alpha f(\alpha)dt \nonumber \\
&=&-\frac{mge}{2A^2kT}\int_0^T\alpha sin(\alpha+\phi)dt \nonumber \\
&=&-\frac{mge}{2A^2kT}\int_0^T\alpha\{sin\alpha cos\phi+cos\alpha sin\phi\}dt \nonumber \\
&=&-\frac{mge}{2A^2kT}\{cos\phi \int_0^T\theta sin\theta dt+sin\phi \int_0^T\theta cos\theta dt\} \nonumber \\
\end{eqnarray}
ここで第5部 数学公式集 5-5より
\begin{eqnarray}
\int_0^T\alpha cos\alpha dt&=&0 \\
\int_0^T\alpha sin\alpha dt &=&ATJ_1(A) \\
\end{eqnarray}
であるから
\begin{eqnarray}
\delta&=&-\frac{mge}{2A^2kT}ATJ_1(A)cos\phi \nonumber \\
&=&-\frac{mge}{2Ak}J_1(A)cos\phi
\end{eqnarray}
となる。
例としてテンプの質量を$80\;[mg]=8\times10^{-5}\;[kg]\;$、ヒゲゼンマイのバネ定数$\;1\times10^{-6}\;[Nm/rad]\;$、
天真ほぞ振れ量$\;e=1\;[\mu m]=1\times10^{-6}\;[m]\;$としたときの振り角と等時性誤差$\;\delta\;$を86400倍して
日差に換算した値との関係を下図に示す。
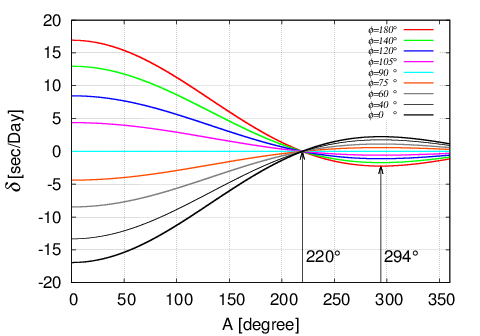
これより天真ほぞの振れは静止時の振れ最大値方向が垂直に近いときが一番影響が大きく、振れ1μmで日差約2秒と
以外と大きな値となることがわかる。静止時の振れ方向が垂直軸と90°のとき等時性誤差への影響が無くなる。
天真ほぞの振れによる等時性誤差は振り角220°のときその影響が無くなり0となる。
また振り角294°(5.136\;rad)のとき最大値をとることがわかる。