固定端ヒゲの問題は3-3-4で求めたオイラー方程式
\begin{eqnarray}
\frac{d^2 \phi}{ds^2}+\lambda sin(\Psi+\phi)-\mu cos(\Psi+\phi)=0
\end{eqnarray}
を解かねばならないが$Goudsmit$等は次のような巧妙な手段を用いて具体的な解の形を求めることなく
目的を達している。
目的は天真を$\;\alpha\;$だけ回転させたときにどれだけ復元モーメントが現れるかということである。
それは天真を$\;\alpha\;$だけ回転させたときにヒゲにどれだけ弾性エネルギーが蓄えられるかを知れば良い。
すなわち3-3-3で求めた
\begin{eqnarray}
U=\frac{kL}{2}\int_0^L(\frac{d\phi}{ds})^2ds
\end{eqnarray}
の$\;U\;$の値を初めのヒゲの形と回転角$\;\alpha\;$とを用いて表せばよいのである。
式(1)は$\;\phi\;$についての2階の微分方程式であるから$\;\phi\;$を求めるには2回の積分を必要とする。
変形後のヒゲの形$\;z_1(s)\;$を求めるには更にもう1回積分しなければならない。
すなわち3回の積分をしなければ変形後のヒゲの形は完全には記述できないが、
さし当り必要な式(2)の中には$\;\phi\;$の形で入っている。
$\;\phi\;$さえ判れば弾性エネルギーは判るのであるからヒゲの変形を完全に求めることなく
1回の積分だけで$\;\phi\;$の値を既知の量を用いて記述しようとするのである。
\begin{eqnarray}
\frac{dx_1}{ds}=cos(\Psi+\phi) \;\;\;\;\;\frac{dy_1}{ds}=sin(\Psi+\phi)
\end{eqnarray}
の関係を式(1)に入れると
\begin{eqnarray}
\frac{d^2 \phi}{ds^2}+\lambda \frac{dy_1}{ds}-\mu \frac{dx_1}{ds}=0
\end{eqnarray}
となるからこれは直ちに積分できて
\begin{eqnarray}
\frac{d\phi}{ds}+\lambda y_1-\mu x_1=C
\end{eqnarray}
を得る。積分定数$\;C\;$を決めるためにこの式をもう1度0から$L$まで積分すると
\begin{eqnarray}
\phi(L)-\phi(0)+\lambda \int_0^Ly_1ds-\mu \int_0^Lx_1ds=CL
\end{eqnarray}
となる。
\begin{eqnarray}
z_1(s)=x_1(s)+iy_1(s) \nonumber
\end{eqnarray}
は変形後のヒゲの形状を表すから
\begin{eqnarray}
\overline{x_1}=\frac{1}{L}\int_0^Lx_1(s)ds\;\;\;\;\;\;\;\;\;\;\overline{y_1}=\frac{1}{L}\int_0^Ly_1(s)ds
\end{eqnarray}
は変形後のヒゲの図心の$\;x\;$座標、$\;y\;$座標を表している。(下図)
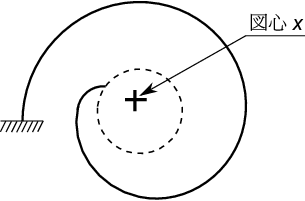
この関係と
\begin{eqnarray}
\phi(0)=\alpha \\
\phi(L)=0
\end{eqnarray}
を式(6)に入れると積分定数$\;C\;$が定まって
\begin{eqnarray}
C=-\frac{\alpha}{L}+\lambda \overline{y_1}-\mu \overline{x_1}
\end{eqnarray}
となる。この$\;C\;$を式(5)に入れると第1積分が
\begin{eqnarray}
\frac{d\phi}{ds}+\lambda (y_1-\overline{y_1})-\mu (x_1-\overline{x_1})=-\frac{\alpha}{L}
\end{eqnarray}
のように得られる。
次に$\;\lambda,\mu\;$を求める。$\;\lambda,\mu\;$は3-3-4で求めた付帯条件式
\begin{eqnarray}
\int_0^Lcos(\Psi+\phi)ds=const. \\
\int_0^Lsin(\Psi+\phi)ds=const.
\end{eqnarray}
の定数値に関連して定まる量である。すなわち3-3-4で求めた
\begin{eqnarray}
z_1(L)-z_1(0)=\int_0^Le^{i(\Psi+\phi)}ds
\end{eqnarray}
の値がヒゲの内外端の距離を示すことから決まってくる。
この式の$\phi$に3-3-4で求めた
\begin{eqnarray}
\phi=\frac{L-s}{L}\alpha
\end{eqnarray}
を入れれば自由端ヒゲの内外端の距離を示すことになる。
自由端ヒゲの外端座標を$z_f(L)$と書くことにすれば
\begin{eqnarray}
z_f(L)-z_1(0)=\int_0^Le^{i\{\Psi+\alpha (L-s)/L\}}ds
\end{eqnarray}
である。内端座標は固定端ヒゲと同じことであるから$\;z_1(0)\;$と書いてある。式(16)と式(14)の差をとると
左辺は自由端ヒゲと固定端ヒゲとの外端座標の差になるからこれは3-3-4で求めたで求めた$\;\Delta\;$に等しい。
すなわち
\begin{eqnarray}
\Delta = \int_0^L\{e^{i\{\Psi+\alpha (L-s)/L\}}-e^{i(\Psi+\phi)}\}ds
\end{eqnarray}
である。
この式を変形して部分積分の公式及び関数の積の微分(第5部 数学公式集 5-2-2)を使えば
\begin{eqnarray}
\Delta&=&\int_0^Le^{i(\Psi+\phi)}\{e^{i\{\alpha (L-s)/L-\phi\}}-1\}ds \nonumber \\
&=&\int_0^L\frac{dz_1}{ds}\{e^{i\{\alpha (L-s)/L-\phi\}}-1\}ds \nonumber \\
&=&[z_1(s)\{e^{i\{\alpha (L-s)/L-\phi\}}-1\}]_0^L \nonumber \\
&\;&-i\int_0^Lz_1(-\frac{\alpha}{L}-\frac{d\phi}{ds})e^{i\{\alpha (L-s)/L-\phi\}}ds
\end{eqnarray}
を得る。
\begin{eqnarray}
\phi(0)=\alpha\;\;\;\;\;\phi(L)=0 \nonumber
\end{eqnarray}
であるから積分の外の部分は消えて
\begin{eqnarray}
\Delta = i\int_0^Lz_1(\frac{\alpha}{L}+\frac{d\phi}{ds})e^{i\{\alpha(L-s)/L-\phi \}}ds
\end{eqnarray}
が得られる。式(14)の代わりにこの式を用いて$\;\lambda,\mu\;$を決めようというのである。
ここで近似を行う。自由端ヒゲと固定端ヒゲとで$\;\phi\;$の形はあまり大きくは違わない(下図参照)としてその差を
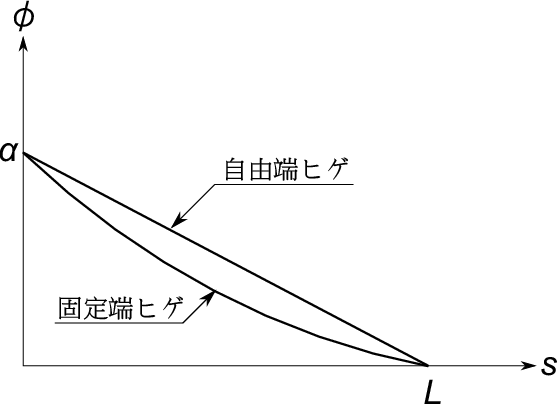
と書くと式(19)の積分の中は
\begin{eqnarray}
z_1\frac{d\varepsilon}{ds}e^{-i\varepsilon}\approx z_1\frac{d\varepsilon}{ds}\{1-i\varepsilon-\frac{\varepsilon^2}{2}+\cdots\}
\end{eqnarray}
となり$\;e\;$の展開の中の第2項以降は$\;\varepsilon\;$の2乗以上の大きさになる。
したがってこれを省略すると式(19)の$\;e\;$の項を1で近似したことになり式(19)は
\begin{eqnarray}
\Delta \approx i\int_0^Lz_1(\frac{\alpha}{L}+\frac{d\phi}{ds})ds
\end{eqnarray}
となる。この式から判るように$\;\Delta\;$は$\;L\varepsilon\;$のオーダーであるから自由端ヒゲの外端変位$\;\Delta\;$が
ヒゲの全長$\;L\;$に比べて小さければ$\;\varepsilon\;$を小さいとした上記の近似が許されるわけで
実際のヒゲではこの条件は常に満たされている。
式(21)の$\;d\phi/ds\;$に式(11)を入れると
\begin{eqnarray}
\Delta=i\int_0^L(x_1+iy_1)\{\mu (x_1-\overline{x_1})-\lambda (y_1-\overline{y_1})\}ds
\end{eqnarray}
となる。
$\;\Delta\;$は自由端ヒゲの外端変位で
\begin{eqnarray}
\Delta \approx \Delta_x+i\Delta_y \nonumber
\end{eqnarray}
のように複素数で表され実数部は$\;x\;$方向の変位、虚数部は$\;y\;$方向の変位を表している。
式(22)の実数部をとると
\begin{eqnarray}
\Delta_x&=&\int_0^L\{\lambda y_1(y_1-\overline{y_1})-\mu y_1(x_1-\overline{x_1})\}ds \nonumber \\
&=&\lambda \int_0^L(y_1^2-y_1\overline y_1)ds-\mu \int_0^L(x_1y_1-y_1\overline x_1)ds \nonumber \\
&=&\lambda( \int_0^Ly_1^2ds-L\overline y_1^2)-\mu (\int_0^Lx_1y_1ds-L\overline x_1\overline y_1)
\end{eqnarray}
となる。
\begin{eqnarray}
I_{hx}&=&\frac{1}{L}\int_0^Ly_1^2ds-\overline{y_1}^2 \nonumber \\
&=&\frac{1}{L}\int_0^L(y_1-\overline y_1)^2ds
\end{eqnarray}
とおくとこれはヒゲの形の図心まわりの断面2次モーメントを意味する。また
\begin{eqnarray}
I_{hxy}&=&\frac{1}{L}\int_0^L x_1y_1ds-\overline{x_1}\overline{y_1} \nonumber \\
&=&\frac{1}{L}\int_0^L (x_1-\overline{x_1})(y_1-\overline{y_1})ds
\end{eqnarray}
とおくとこれは図心まわりの断面1乗積で上下左右対称であれば0になる量である。
実際のヒゲの形は変形後は完全な対称図形ではないがここでは近似的にこれを0としておく。
完全に対称でなくても$\;I_{hx}\;$に比べれば$\;I_{hxy}\;$は充分に小さいからこれを省略するという意味である。
これらの関係を式(23)に入れると
\begin{eqnarray}
\Delta_x=\lambda LI_{hx}
\end{eqnarray}
となる。同様に式(22)の虚数部から
\begin{eqnarray}
\Delta_y=\mu LI_{hy}
\end{eqnarray}
を得る。変形後のヒゲの形がほぼ対称であれば
\begin{eqnarray}
I_{hx}=I_{hy}=I_h
\end{eqnarray}
とおくことができる。
したがって
\begin{eqnarray}
\lambda=\frac{\Delta_x}{LI_h}\;\;\;\;\;\mu=\frac{\Delta_y}{LI_h}
\end{eqnarray}
となり未定定数$\;\lambda,\mu\;$が自由端ヒゲの外端変位で表されることになった。
これを式(11)に入れて
\begin{eqnarray}
\frac{d\phi}{ds}=-\frac{\alpha}{L}+\frac{1}{LI_h}\{\Delta_y(x_1-\overline{x_1})-\Delta_x(y_1-\overline{y_1})\}
\end{eqnarray}
を得る。右辺の第1項は自由端ヒゲの$\;d\phi/ds\;$の値であり、第2項がそれからのずれを表す量で
先に$\;d\varepsilon /ds\;$と書いた部分である。
$\;\Delta\;$が十分小さければ第2項は第1項の補正項となりこれまで用いた近似が許される。
式(30)を弾性エネルギーの式(2)に入れると
\begin{eqnarray}
U&=&\frac{k}{2L}\int_0^L\{-\alpha+\frac{\Delta_y(x_1-\overline{x_1})-\Delta_x(y_1-\overline{y_1})}{I_h}\}^2ds \nonumber \\
&=&\frac{k}{2L}\int_0^L[\alpha^2-\frac{2\alpha}{I_h}\{\Delta_y(x_1-\overline{x_1})-\Delta_x(y_1-\overline{y_1})\} \nonumber \\
&\;&\;+\frac{1}{I_h^2}\{\Delta_y^2(x_1-\overline{x_1})^2+\Delta_x^2(y_1-\overline{y_1})^2-2\Delta_x\Delta_y(x_1-\overline{x_1})(y_1-\overline{y_1})\}]ds \nonumber \\
\end{eqnarray}
となるが式(7)(24)(25)の関係を入れると
\begin{eqnarray}
U=\frac{k}{2}(\alpha^2+\frac{\Delta_x^2+\Delta_y^2}{I_h})
\end{eqnarray}
となる。この式の最後の項は$\;\Delta\;$の実数部と虚数部の自乗和であるからこれを
\begin{eqnarray}
|\Delta|^2 = \Delta_x^2+\Delta_y^2
\end{eqnarray}
と書くことにすれば
\begin{eqnarray}
U=\frac{k}{2}(\alpha^2+\frac{|\Delta|^2}{I_h})
\end{eqnarray}
となる。かくして天真を$\;\alpha\;$だけ回転したときにヒゲに蓄えられる弾性エネルギーが
回転角$\;\alpha\;$と自由端条件を与えたら動くはずの距離$\;\Delta\;$を用いて表された。
$\;\Delta\;$は3-3-4の式(18)により最初のヒゲの形$\;z(s)\;$が与えられれば計算出来る量であるから
$\;U\;$が$\;\alpha\;$の関数として求まったことになる。
変形後のヒゲの形$\;z_1(s)\;$を具体的に求めることなく、自由端ヒゲの外端変位という量を用いて
弾性エネルギー、したがってまた復元力を求めるという考え方は実に巧妙である。