ある形状のヒゲが与えられたとき、天真を$\;\alpha\;$だけ回転させたらヒゲはどのような形に
変形するかという問題を考える。
3-3-2の記号を使えば$\;z(s)\;$が与えられたとき$\;z_1(s)\;$を求めよという問題である。
これは$\;\Psi(s)\;$が与えられたとき$\;\phi(s)\;$を求めよという問題と考えてもよい。
内端すなわち$\;s=0\;$では$\;z_1\;$は$\;z(0)\;$の位置から角$\;\alpha\;$だけ回転した位置であるから
\begin{eqnarray}
z_1(0)=z(0)e^{i\alpha}
\end{eqnarray}
である。また外端は止めてあるから位置は変化しない。すなわち
\begin{eqnarray}
z_1(L)=z(L)
\end{eqnarray}
である。接線の方向を表す$\;\Psi+\phi\;$を考えると内端ではヒゲ玉から外へ向かう角度は
一定のまま天真が回転するから方向角は回転によって$\;\alpha\;$だけ増加する。したがって
\begin{eqnarray}
\phi(0)=\alpha
\end{eqnarray}
である。また外端は止めてるがその方向も回転によって影響されないよう固定してあるとすれば
接線の方向に変化がないから
\begin{eqnarray}
\phi(L)=0
\end{eqnarray}
となる。
天真が回転することによってヒゲに与える拘束はこれだけである。
すなわち内端と外端の位置および傾斜を指定し、ヒゲの途中の部分には何も束縛を与えていない。
この条件の下にヒゲはどのような形をとるかという問題は、この条件を満たす範囲内で3-3-3で求めた弾性エネルギー
\begin{eqnarray}
U=\frac{kL}{2}\int_0^L(\frac{d\phi}{ds})^2ds
\end{eqnarray}
が最小になるような形を求めることに相当する。
すわわち式(1)〜(4)の4つの条件の下に式(5)なる積分値を最小にするような
$\;\phi\;$を求めようという問題である。
式(5)の中の未知関数は$\;\phi\;$だけであるから両端の条件も$\;\phi\;$に関するものだけ、
すなわち式(3)と式(4)だけであれば数学的には比較的易しい問題である。
現実には$\;\phi\;$を積分した値$z$に関する2つの条件、式(1)と(2)が存在するので
かなり厄介な問題になる。そこでこの問題を解くための足がかりとして先ず式(1)(2)を棚上げし
式(3)(4)だけの条件の下に式(5)の積分値を最小にするような$\;\phi\;$を求めてみることにしよう。
$Goudsmit$等はこのようなヒゲを自由端ヒゲと名づけた。
自由端ヒゲの解を求める前にこの問題の物理的意味を考察しておこう。
$\;\phi\;$と$\;z_1\;$との関係は3-3-2から
\begin{eqnarray}
\frac{dz_1}{ds}=e^{i(\Psi+\phi)}
\end{eqnarray}
であるから$\;\phi\;$から$\;z_1\;$を求めるには積分操作を伴う。
このとき積分定数が入ってくるからこれを適当に選ぶことによって式(1)か式(2)の何れか一方は
満たしておくことが出来る。したがって自由端ヒゲと通常のヒゲとの拘束条件の違いは1つだけである。
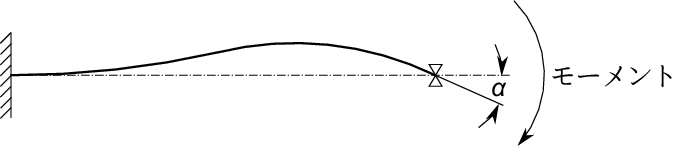
積分定数で外端条件を満たさせると考えるとこれは丁度直線梁における下図のような問題に対応する。
先端を支持した片持ち梁の先端にあるモーメントを加えると図のように変形するであろう。
先端の傾斜角$\;\alpha\;$を知って変形の形を求めよという問題である。
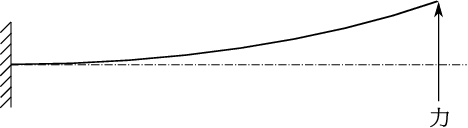
これを解くにあたって2番目の図、3番目の図のような2つの問題に分解して考える。
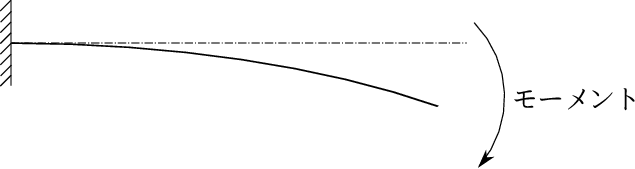
すなわち先ず2番目の図のように片持ち梁の先端にモーメントを加えた問題を解く。
これは簡単に解けるが図のように先端にたわみを生ずる。そこでたわみを打ち消すように先端に力を加える。
重ね合わせの原理が成立するから3番目の図のように先端に力を加えたときの問題を解いておいて
重ね合わせれば最初の図の問題の解になる。
自由端ヒゲの問題はこの第1段階の部分に相当する。ヒゲの内端が片持ち梁の先端、外端が固定端である。
内端位置の条件、式(1)を落とすというのはモーメントを加えることにより天真位置が移動してしまう
ということを意味する。
どれだけ移動するかを計算しておいて第2段階で天真位置を元に戻すような力を加えるのである。
このモデルに自由端ヒゲという名称を与えるのは少し奇妙ではあるが、この名を考えるときは内端条件、
式(1)を満たすように積分定数を定めるとして外端条件、式(2)を外した場合を想定する方がよい。
天真はその位置で回転する。このときヒゲの外端は固定されておらずその位置は自由に動ける。
ただ傾斜だけは初めの方向を常に保っているものとする。外端が自由に動けるヒゲという意味で
自由端ヒゲと名づけたが完全に自由なのではなく方向だけは最初の方向を保たされているのである。
片持ち梁のモデルで言えば2番目の図の右端の位置が原点にくるように座標軸全体を下げて考えることに相当する。
モーメントを加えた右端はモーメントによって方向は変えるが位置は変えない。
右端は固定端ではなく方向だけ水平に保って位置は自由に動けるというモデルになる。
自由端ヒゲの解は容易に得られる。直線梁の先端にモーメントを加える問題では梁の全長にわたってモーメント一定、
したがって全長にわたって曲率が一定になる。
曲がり梁の先端にモーメントを加える問題では全長にわたって曲率変化が一定である。
現在の問題では曲率変化は3-3-2から
\begin{eqnarray}
\frac{1}{\rho_1}-\frac{1}{\rho}=\frac{d\phi}{ds}
\end{eqnarray}
であるから全長にわたって
\begin{eqnarray}
\frac{d\phi}{ds}=const.
\end{eqnarray}
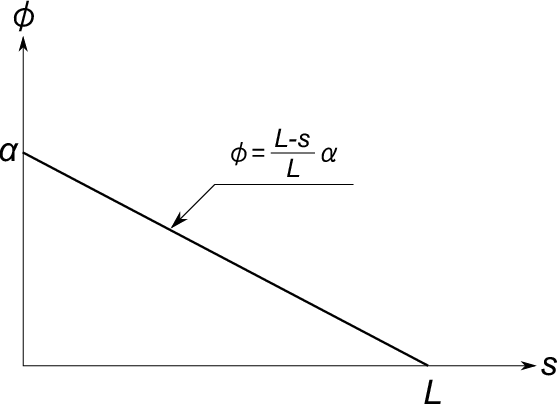
という解が得られるであろう。内端と外端の条件、式(3)と式(4)を用いれば式(8)からは容易に
\begin{eqnarray}
\phi=\frac{L-s}{L}\alpha
\end{eqnarray}
が得られる(下図)。
この$\phi$が式(5)の積分を最小にするものであることは次のようにして説明できる。
いま
\begin{eqnarray}
\phi=\frac{L-s}{L}\alpha+\varepsilon(s)
\end{eqnarray}
が積分を最小とする関数であるとしよう。両端の条件から
\begin{eqnarray}
\varepsilon(0)=\varepsilon(L)=0
\end{eqnarray}
である。
\begin{eqnarray}
(\frac{d\phi}{ds})^2=\{-\frac{\alpha}{L}+\frac{d\varepsilon}{ds}\}^2=(\frac{\alpha}{L})^2-2\frac{\alpha}{L}\frac{d\varepsilon}{ds}+(\frac{d\varepsilon}{ds})^2
\end{eqnarray}
であるから
\begin{eqnarray}
\int_0^L(\frac{d\phi}{ds})^2ds=\frac{\alpha^2}{L}-\frac{2\alpha}{L}\{\varepsilon(L)-\varepsilon(0)\}+\int_0^L(\frac{d\varepsilon}{ds})^2ds
\end{eqnarray}
となる。右辺の第2項は式(11)によって0であり、第3項は$\;\varepsilon=0\;$の場合に最小である。
したがって式(9)の$\;\phi\;$が積分、式(5)を最小にする$\;\phi\;$である。
ここで内端条件を保たせた場合の自由端ヒゲの外端変位を求めておこう。変形後の外端変位は式(6)を積分して
\begin{eqnarray}
z_1(L)=z_1(0)+\int_0^Le^{i(\Psi+\phi)}ds
\end{eqnarray}
である。積分の中を3-3-2の
\begin{eqnarray}
\frac{dz}{ds}=e^{i\Psi}
\end{eqnarray}
を用いて変形した後、部分積分(第5部 数学公式集5-2-4)を行うと式(3)(4)より$\;\phi(L)=0,\phi(0)=\alpha\;$だから
\begin{eqnarray}
z_1(L)&=&z_1(0)+\int_0^L\frac{dz}{ds}e^{i\phi}ds \nonumber \\
&=&z_1(0)+[ze^{i\phi}]_0^L-i\int_0^Lze^{i\phi}\frac{d\phi}{ds}ds
\end{eqnarray}
となる。
更に$\phi$として式(9)を入れると
\begin{eqnarray}
z_1(L)=z_1(0)+z(L)-z(0)e^{i\alpha}+i\int_0^Lz(s)exp\{i\alpha (L-s)/L\}\frac{\alpha}{L}ds
\end{eqnarray}
となり、更に内端条件式(1)から右辺の第1項と第3項とが等しくなって結局外端変位$\;\Delta\;$は
\begin{eqnarray}
\Delta&=&z_1(L)-z(L) \nonumber \\
&=&i\frac{\alpha}{L}e^{i\alpha}\int_0^Lz(s)exp\{-i\alpha s/L\}ds
\end{eqnarray}
で与えられる。変形前のヒゲの形$\;z(s)\;$が与えられればこの積分を行うことによって自由端条件にした場合の
外端の変位が求められる。
式(18)は複素数でその実部、虚部が$\;x\;$方向、$\;y\;$方向の変位になる。
ヒゲの外端が動けるようになっていれば$\;\phi\;$は式(9)のような簡単な形をとり、
これを基にして弾性エネルギーや復元モーメントも容易に計算できる。
実際には外端が固定されているのでこの条件が追加され$\;\phi\;$の形も式(9)とは異なったものとなる。
前に述べたように式(6)を積分するときの積分定数の選び方によって内端条件式(1)か
外端条件式(2)の一方だけはいつでも満たさせておくことができる。
思考の便宜に応じてそのどちらかをとってきたのであるが、この積分定数は$\;z_1\;$の座標原点を
どこにとるかというだけの意味を持つものであるから内端外端2つの条件を与えるということを
その相対位置が与えられているという1つの条件に置き換えてしまえば上の積分定数の意味を
考える必要がなくなる。
相対位置は
\begin{eqnarray}
z_1(L)-z_1(0)=\int_0^Le^{i(\Psi+\phi)}ds
\end{eqnarray}
でこの値が式(1)(2)からわかるように
\begin{eqnarray}
z(L)-z(0)e^{i\alpha}
\end{eqnarray}
に等しいというのが外端固定の条件になる。
式(20)はヒゲの最初の内外端位置と回転角$\;\alpha\;$とから定まる定数であるから式(19)の積分がある定数に
等しいというのが外端固定の条件である。式(19)を実部虚部に分けて書けば
\begin{eqnarray}
\int_0^Lcos(\Psi+\phi)ds=const. \\
\int_0^Lsin(\Psi+\phi)ds=const.
\end{eqnarray}
となる。この条件と内外端の傾斜条件
\begin{eqnarray}
\phi(0)&=&\alpha\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3) \nonumber \\
\phi(L)&=&0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(4) \nonumber
\end{eqnarray}
のもとに
\begin{eqnarray}
\frac{2U}{kL}=\int_0^L(\frac{d\phi}{ds})^2ds
\end{eqnarray}
なる積分を最小にするよう$\;\phi(s)\;$を求めよという問題である。
未知関数を含んだある定積分の値を最小にするよう未知関数の関数形を決める問題を変分問題という。
未知関数に与えられる条件としては式(3)(4)のように境界における値だけを与える場合が多いが、
現在の問題のように未知関数$\;\phi\;$に式(21)(22)のような余分の条件を付けられることもある。
このような問題を条件付変分問題と呼んでいる。
条件がない場合の式(23)を最小にする$\;\phi\;$は
\begin{eqnarray}
\frac{d\phi}{ds}=const.
\end{eqnarray}
すなわち
\begin{eqnarray}
\frac{d^2 \phi}{ds^2}=0
\end{eqnarray}
なる微分方程式の解と同じであった。式(25)を式(3)(4)なる境界条件の許に解けば
式(9)が得られる。これに対し式(21)(22)なる条件が付加されているときの変分問題の解は
\begin{eqnarray}
\frac{d^2 \phi}{ds^2}+\lambda sin(\Psi+\phi)-\mu cos(\Psi+\phi)=0
\end{eqnarray}
なる微分方程式の解になる(第5部 数学公式集5-7 , 5-8参照)。



