図のようにテンプが静止した状態で垂直方向から角度$\;\phi\;$だけ傾いた方向で半径$\;r\;$のところに
質量$\;m\;$の片重り(テンワの回転中心と重心位置とのズレ)があるとき、テンプに掛かる片重りによるトルク$\;f(\alpha)\;$は
テンプの回転角$\;\alpha\;$によって変化し次式で表される。
\begin{eqnarray}
f(\alpha)=mgrsin(\alpha+\phi)
\end{eqnarray}
ここで$\;g\;$は重力加速度である。
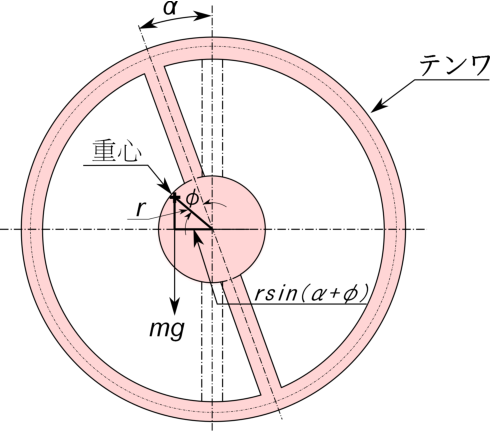
このときのテンプの運動方程式はテンワの慣性モーメント$\;I\;$,ヒゲゼンマイのバネ定数$\;k\;$として次のように表される。
\begin{eqnarray}
I\frac{d^2 \alpha}{dt^2}&=&f(\alpha)-k\alpha \\
I\frac{d^2 \alpha}{dt^2}&=&mgrsin(\alpha+\phi) -k\alpha
\end{eqnarray}
すなわちこれは$\;\alpha\;$を$\;\theta\;$と置き換えれば3-1の外乱トルク$\;f(\theta)\;$が加わったときのテンプの運動方程式と同じである。
外乱トルク$\;f(\theta)\;$があるときの等時性誤差は
\begin{eqnarray}
\delta=-\frac{1}{A^2kT}\int_0^T\theta f(\theta) dt
\end{eqnarray}
であったから今回は次のようになる。
\begin{eqnarray}
\delta&=&-\frac{1}{A^2kT}\int_0^T\alpha f(\alpha)dt \nonumber \\
&=&-\frac{1}{A^2kT}\int_0^T\alpha mgrsin(\alpha+\phi)dt \nonumber \\
&=&-\frac{mgr}{A^2kT}\int_0^T\alpha sin(\alpha+\phi)dt
\end{eqnarray}
ここで$\;\alpha\;$はテンワの回転角であり$\;f(\alpha)\;$が小さければ近似的に
\begin{eqnarray}
\alpha=Asin\omega t
\end{eqnarray}
とおくことが出来る。これを式(5)に入れて三角関数の加法定理(第5部 数学公式集 5-1-4)を使えば
\begin{eqnarray}
\delta&=&-\frac{mgr}{A^2kT}\int_0^TAsin\omega t \;sin(Asin\omega t+\phi)dt \nonumber \\
&=&-\frac{mgr}{A^2kT}\int_0^TAsin\omega t\;\{sin(Asin\omega t)\;cos\phi)+cos(Asin \omega t)\;sin\phi\}dt \nonumber \\
&=&-\frac{mgr}{A^2kT}\{cos\phi \int_0^TAsin\omega t\;sin(Asin\omega t) dt+sin\phi \int_0^TAsin\omega t\;cos(Asin \omega t)dt\}
\end{eqnarray}
となる。
ここで第5部 数学公式集 5-5より
\begin{eqnarray}
\int_0^T\alpha cos\alpha dt&=&0 \\
\int_0^T\alpha sin\alpha dt &=&ATJ_1(A)
\end{eqnarray}
であるから式(7)は
\begin{eqnarray}
\delta=-\frac{mgr}{Ak}cos\phi J_1(A)
\end{eqnarray}
となる。2-1より
\begin{eqnarray}
T=2\pi \sqrt{\frac{I}{k}} \\
k=(\frac{2\pi}{T})^2I
\end{eqnarray}
であるから式(10)は
\begin{eqnarray}
\delta=-(\frac{T}{2\pi})^2\frac{mgr}{I}\frac{J_1(A)}{A}cos\phi
\end{eqnarray}
となる。この式の変数部分$\;-J_1(A)/A\;cos\phi\;$をグラフにすると図のようになる。
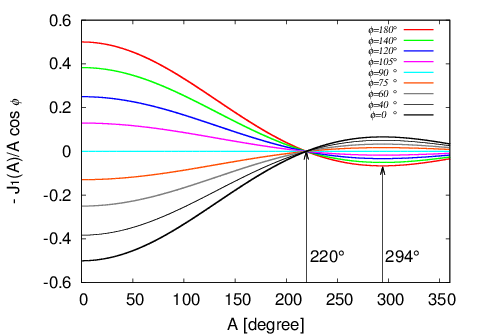
式(13)より静止時の片重りの位置が垂直上方なら$\;\phi=0\;$すなわち$\;cos\phi=1\;$となり片重りによる影響は最大になる。
この場合等時性誤差は図の$\;\phi=0\;$の曲線のとおりになり、振り角220°(正確には219.5405804°)で0になる。
また振り角294°でこれは最大値をとり、片重り位置が垂直軸に対して90°のときは片重りの影響が出ない。
図からわかるようにテンワの片重りは振り角220°では姿勢差が現れない。したがって片重りをとるときには
ゼンマイをほどいて振り角を165°あるいは135°などと低くして重りをとることが推奨される。
実際の調整の際、テンワの片重りに関してはこの理論と実際とはよく一致している。