3-3-6より
\begin{eqnarray}
\delta=\frac{1}{2A^2TI_h}\int_0^T\alpha \frac{d|\Delta|^2}{d\alpha}dt
\end{eqnarray}
等時性を良くするには$\;\delta\;$が振り角$\;A\;$によらない定数であればよい。0であっても勿論よい。
式(1)の右辺は積分の外に$\;A^{-2}\;$があるから積分の値が$\;A^2\;$に比例する量になれば$\;\delta\;$は
振り角によらないことになる。ここで等時性のよいヒゲの形を求めるにあたって2つの方針が立つ。
第1は$\;\Delta\;$を0にし、したがって$\;\delta\;$を0にするという方針である。第2は$\;\Delta\;$は0ではないが
式(1)の積分を$\;A^2\;$に比例させて$\;\delta\;$を定数にしようという方針である。$Re'sal$や$Caspari$は
後者の方針にしたがってひげ形状の設計を論じた。
一方$Edouard\; Phillips$は前者の方針にしたがって等時性のよいヒゲ形状を求めた。本節ではこれについて説明する。
ヒゲの全長を$\;L\;$としこれを$\;(0,l_1),(l_1,L-l_2),(L-l_2,L)\;$なる3つの部分に分けて考える。
$\;l_1,l_2\;$は$\;L\;$に比べれば小さい値で第1の部分を内側の端末曲線、第3の部分を外側の端末曲線と呼ぶことにする。
3-3-4で求めた外端変位
\begin{eqnarray}
\Delta&=&z_1(L)-z(L) \nonumber \\
&=&i\frac{\alpha}{L}e^{i\alpha}\int_0^Lz(s)exp\{-i\alpha s/L\}ds
\end{eqnarray}
の積分をこれに応じて3つに分け
\begin{eqnarray}
\Delta_1&=&i\frac{\alpha}{L}e^{i\alpha}\int_0^{l_1}z(s)e^{-i\alpha s/L}ds \\
\Delta_2&=&i\frac{\alpha}{L}e^{i\alpha}\int_{l_1}^{L-l_2}z(s)e^{-i\alpha s/L}ds \\
\Delta_3&=&i\frac{\alpha}{L}e^{i\alpha}\int_{L-l_2}^{L}z(s)e^{-i\alpha s/L}ds \\
\Delta&=&\Delta_1+\Delta_2+\Delta_3
\end{eqnarray}
とする。第2の部分がヒゲの主要部で、この部分は3-4-1で論じたアルキメデス曲線をしているとする。
フィリップスはこの部分をヘリカルスプリングとして計算し$Goudsmit$もこれを引用しているが、現在は平ヒゲの方が
多く用いられているし3-4-1の計算を引用するにも便利であるのでアルキメデス曲線として計算する。
そうすると$\;\Delta_2\;$の計算は3-4-2で求めた外端変位$\;\Delta\;$の結果がそのまま用いられて
\begin{eqnarray}
\Delta_2=\frac{a^2}{L}\alpha[\theta_1^2exp\{i\theta_1\}-\theta_0^2exp\{i(\alpha+\theta_0)\}]
\end{eqnarray}
となる。
$\;\theta_0\;$および$\;\theta_1\;$は3-4-2の式(15)ではヒゲの巻き始め及び巻き終わり点における
アルキメデス曲線の$\;\theta\;$の値であったが、式(7)では$\;l_1\;$点および$\;L-l_2\;$点における$\;\theta\;$の値を意味する。$\;\Delta\;$の積分は
\begin{eqnarray}
s=L-\sigma
\end{eqnarray}
と置き換えて外端から逆向きに積分することにすると
\begin{eqnarray}
\Delta_3&=&i\frac{\alpha}{L}e^{i\alpha}\int_0^{l_2}z(L-\sigma)e^{-i\alpha(L-\sigma)/L}d\sigma \nonumber \\
&=&i\frac{\alpha}{L}\int_0^{l_2}z(L-\sigma)e^{i\alpha \sigma/L}d\sigma
\end{eqnarray}
となる。これらを式(6)に入れると
\begin{eqnarray}
\Delta&=&\frac{a^2}{L}\alpha[\theta_1^2exp\{i\theta_1\}-\theta_0^2exp\{i(\alpha+\theta_0)\}] \nonumber \\
&\;&+i\frac{\alpha}{L}e^{i\alpha}\int_0^{l_1}z(s)e^{-i\alpha s/L}ds \nonumber \\
&\;&+i\frac{\alpha}{L}\int_0^{l_2}z(L-\sigma)e^{i\alpha \sigma/L}d\sigma
\end{eqnarray}
が得られる。ここで
\begin{eqnarray}
\frac{a^2}{L}\alpha \theta_0^2exp\{i(\alpha+\theta_0)\}&=&i\frac{\alpha}{L}e^{i\alpha}\int_0^{l_1}z(s)e^{-i \alpha s/L}ds \nonumber \\
\frac{a^2}{L}\alpha \theta_1^2exp\{i\theta_1\}&=&-i\frac{\alpha}{L}\int_0^{l_2}z(L-\sigma)e^{i \alpha \sigma/L}d\sigma
\end{eqnarray}
であれば式(10)の$\;\Delta\;$は0となる。すわわち
\begin{eqnarray}
i\int_0^{l_1}z(s)e^{-i \alpha s/L}ds&=&a^2\theta_0^2exp\{i\theta_0\} \\
i\int_0^{l_2}z(L-\sigma)e^{i \alpha \sigma/L}d\sigma&=&-a^2\theta_1^2exp\{i\theta_1\}
\end{eqnarray}
であればよい。
\begin{eqnarray}
R_0=a\theta_0
\end{eqnarray}
とおけばこれは$\;l_1\;$点すなわちヒゲの内端曲線の部分からアルキメデス曲線へ移る点の半径を意味する。
同様に
\begin{eqnarray}
R_1=a\theta_1
\end{eqnarray}
はアルキメデス曲線から外端曲線へ移る点の半径である。これらを使えば式(12)(13)は
\begin{eqnarray}
\int_0^{l_1}z(s)e^{-i \alpha s/L}ds&=&-iR_0^2exp\{i\theta_0\} \\
\int_0^{l_2}z(L-\sigma)e^{i \alpha \sigma/L}d\sigma&=&iR_1^2exp\{i\theta_1\}
\end{eqnarray}
となる。左辺の積分の中にある$\;s,\sigma\;$の変域は$\;(0,l_1),(0,l_2)\;$で$\;l_1,l_2\;$は$\;L\;$に比べて小さい値であるから
$\;s/L,\sigma/L\;$は何れも1に比べて小さい値になる。そこで
\begin{eqnarray}
e^{-i \alpha s/L}=1-i\alpha \frac{s}{L}+\cdots \\
e^{i \alpha \sigma/L}=1+i\alpha \frac{\sigma}{L}+\cdots
\end{eqnarray}
と展開してその第1項だけを取ることにすると
\begin{eqnarray}
\int_0^{l_1}z(s)ds&=&-iR_0^2e^{i\theta_0} \\
\int_0^{l_2}z(L-\sigma)d\sigma&=&iR_1^2e^{i\theta_1}
\end{eqnarray}
が得られる。
式(20)の左辺を$\;l_1\;$で割ったものは内端曲線の重心座標になる。したがって式(20)は内端曲線の重心座標が
$\;\theta_0\;$の方向から-90°の方向、$\;R_0^2/l_1\;$なる距離にあることを意味する。
$\;\theta_0\;$の方向に$\;x_1\;$座標をとり$\;z(s)\;$を$\;x_1\;$軸を実軸とする複素平面で表示することにすれば式(20)は
\begin{eqnarray}
\frac{1}{l_1}\int_0^{l_1}z(s)ds=-i\frac{R_0^2}{l_1}
\end{eqnarray}
あるいは
\begin{eqnarray}
\frac{1}{l_1}\int_0^{l_1}x_1(s)ds&=&0 \\
\frac{1}{l_1}\int_0^{l_1}y_1(s)ds&=&-\frac{R_0^2}{l_1}
\end{eqnarray}
となる。これがフィリップスの条件で図はこの条件を満たす端末曲線の一例である。図の$\;AB\;$部が内端曲線でこの重心が$\;G\;$である。
$\;B\;$から外側はアルキメデス曲線になっているものとする。
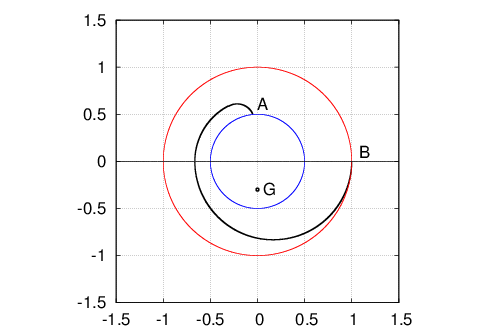
同様に式(21)は外端曲線の重心が$\;\theta_1\;$の方向から90°進んだ方向、$\;R_1^2/l_2\;$なる距離にあることを示している。
$\;\theta_1\;$方向に$\;x_2\;$軸をとり外端曲線を$\;x_2\;$を実軸とする複素平面に表示することにすれば式(21)は
\begin{eqnarray}
\frac{1}{l_2}\int_0^{l_2}z(L-\sigma)d\sigma=i\frac{R_1^2}{l_2}
\end{eqnarray}
となる。
式(22)で$\;s\;$の原点を$\;l_1\;$点にとりここから内側に内端曲線を測ることにすると$\;y_1\;$軸の方向が逆になるから式(22)は
\begin{eqnarray}
\frac{1}{l_1}=\int_0^{l_1}z(s)ds=i\frac{R_0^2}{l_1}
\end{eqnarray}
となる。
また式(22)で外端曲線の長さを$\;L-l_2\;$点から測って$\;s\;$とすれば
\begin{eqnarray}
\frac{1}{l_2}=\int_0^{l_2}z(s)ds=i\frac{R_1^2}{l_2}
\end{eqnarray}
となる。式(23)と式(24)は同じ形であるからサフィックスを外してまとめて
\begin{eqnarray}
\frac{1}{l}\int_0^lz(s)ds=i\frac{R^2}{l}
\end{eqnarray}
と書くことができる。これがフィリップスの条件で
「端末曲線の重心座標がアルキメデス曲線と接する点から端末の方に測って90°の方向、$\;R^2/l\;$の距離にある。
ここで$\;R\;$はアルキメデス曲線と端末曲線の接する半径、$\;l\;$は端末曲線の長さである。」
と表現することが出来る。
例として半径$\;R\;$なる半円は長さが$\;\pi R/2\;$であり、重心点は中心から$\;2R/\pi\;$のところにあるからフィリップスの条件、
式(28)を満たしている。すなわち内端曲線も外端曲線も半円にしてやればよい。しかし半円にするとアルキメデス曲線から
半ピッチのところに端末が来るからこれでは実用上固定に不便である。
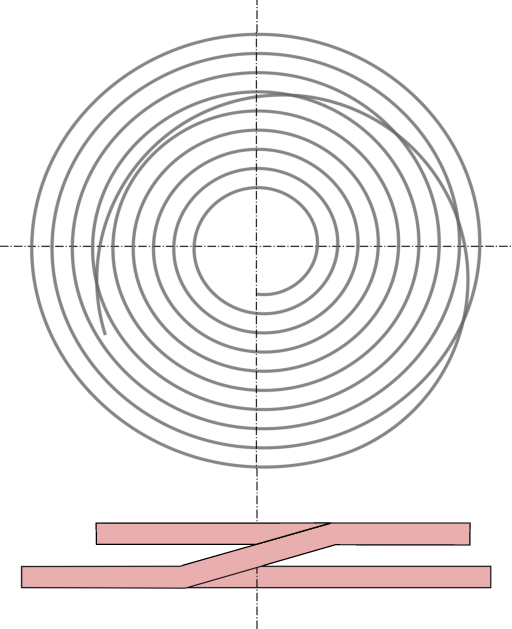
端末曲線に270°程度の角度を与えると、重心が$\;y\;$軸上にあるためには図に見るように右半分に比べて左半分はずっと
原点に近づいた形をとる。内端曲線としてはこのような形が便利で実用されている。
外端曲線についても同様でフィリップスの条件を満たさせようとすると曲線が半径$\;R\;$より内側に入ってきて内側にある
アルキメデス曲線とぶつかってしまう。それでやむを得ず外端部を少し持ち上げて図のようにして端末曲線を作る。
このようにして作ったヒゲを巻上げヒゲという。
式(7)において$\;\theta_1^2\;$は$\;\theta_0^2\;$の10倍くらいの値をもっている。$\;\theta_1\;$の影響を外端曲線で、
$\;\theta_0\;$の影響を内端曲線で消しているのであるから外端曲線の役目の方が内端曲線の役目よりずっと大切である。
内端曲線はヒゲ玉に取り付ける部分の曲線で寸法の一番小さい部分であるからこの形を計算で正確に指定しても
その通りに作ることは困難である。
作業が困難なことと重要性が少ないこととを考慮して一般には内端曲線にはおよその形を与えるだけであまりやかましくは
整えないのが普通である。フィリップスの条件は重心位置だけを問題にしているからこれを満足する形は無限に存在する。