本節は小牧昭一郎氏の論文「等時性誤差(4)」からの抜粋である。
テンワの片重り理論では振り角が220°のとき姿勢差が出ないが、実際には振り角220°で姿勢差が無くなることはない。
その一番の原因はヒゲゼンマイの重心移動の問題である。これには先ずヒゲの内端点付近の運動を考える必要がある。
ヒゲの内端点はヒゲ玉に取り付けられているからいくら回転してもここは半径方向には動かない。
ヒゲ玉が回転するにつれてヒゲの1,2,3巻目くらいに関してはヒゲは内端点付近では半径方向にほとんど移動しない。
つまり拡がりも近づきもしない。これに対し、ヒゲ取付点と反対の方向、すなわち180°回転した方向のヒゲは
巻き締められたときはヒゲ玉に近づいてくるし、ほどかれたときは遠のいていく。
これは通常の平ヒゲの外端付近の運動と同様である。
ヒゲの外端、つまり緩急針と天真の間にあるヒゲは半径方向にはほとんど動かない。
振り角に応じてピッチが伸縮するということはない。
これに対し緩急針と反対側のヒゲは巻き締められれば大いに縮まるし、ほどけるときにはおおきく拡がっていく。
したがって内端付近の重心点は巻き締めたときは内端点に近づき、ほどけたときは内端点と反対方向へ移動する。
この様子を下図に示す。
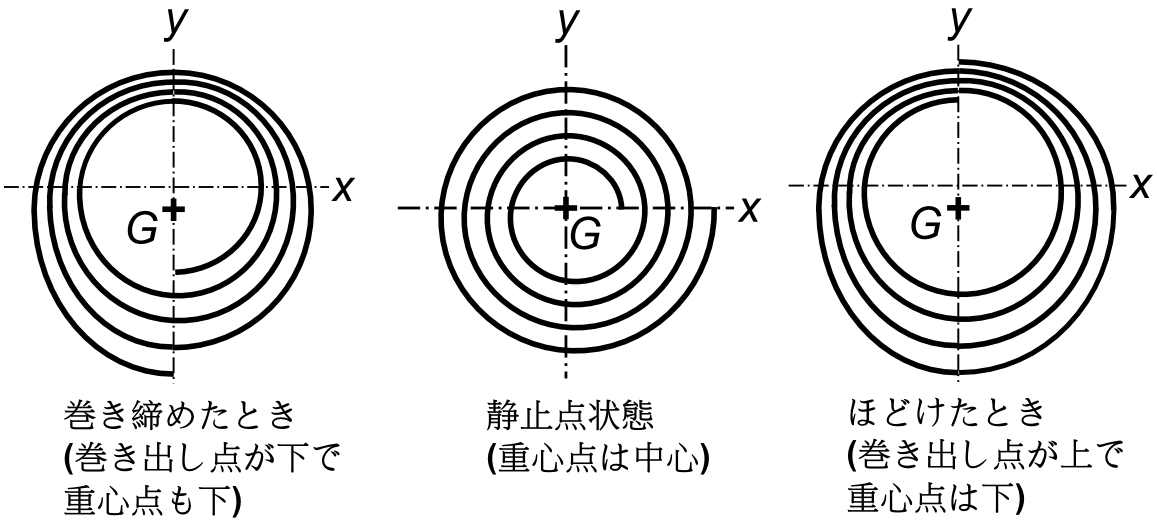
静止時の内端点を$\;x\;$軸の+の方向、紙面上右水平方向に書いたのでテンプが回転して内端点が図のように
90°回転したとき、つまり巻き締めたときもほどけたときも垂直下方に伸びることになる。
つまりヒゲの重心点$\;G\;$が紙面上、下方に移動するのである。このときの重心点移動の軌跡を図で表せば
下図のようになる。尚、$\;x\;$軸はヒゲ内端点とヒゲ玉中心を結ぶ線である。
ヒゲゼンマイの重心点$\;G\;$は$S.Goudsmit$と$M.Wang$によって自由外端ヒゲに関し次のように表されている。
\begin{eqnarray}
G=G_x+iG_y=-i\frac{\delta \Delta}{\delta \alpha}
\end{eqnarray}
この$\Delta$に3-4-2で求めた
\begin{eqnarray}
\Delta=\frac{a^2}{L}\alpha[\theta_1^2exp\{i\theta_1\}-\theta_0^2exp\{i(\alpha+\theta_0)\}]
\end{eqnarray}
すなわち自由外端平ヒゲの外端変位を代入すると
\begin{eqnarray}
G&=&-i\frac{d}{d\alpha}\{\frac{a^2\alpha}{L}[\theta_1^2exp\{i\theta_1\}-\theta_0^2exp\{i(\alpha+\theta_0)\}] \nonumber \\
&=&-i\frac{a^2\theta_1^2}{L}e^{i\theta_1}+i\frac{a^2\theta_0^2}{L}e^{i(\alpha+\theta_0)}-\frac{a^2\theta_0^2}{L}\alpha e^{i(\alpha+\theta_0)}\;\;\;\;\;\;\;\;\;\;\;\;
\end{eqnarray}
ここで$-i\frac{a^2\theta_1^2}{L}e^{i\theta_1}$はヒゲが固定されたことにより発生する重心点の変位であるから、これを省略すると
\begin{eqnarray}
G'&=&i\frac{a^2}{L}\theta_0^2e^{i(\alpha+\theta_0)}-\frac{a^2}{L}\theta_0^2\alpha e^{i(\alpha+\theta_0)} \nonumber \\
&=&i\frac{a^2\theta_0^2}{L}\{cos(\alpha+\theta_0)+isin(\alpha+\theta_0)\}-\frac{a^2\theta_0^2}{L}\alpha\{cos(\alpha+\theta_0)+isin(\alpha+\theta_0)\} \nonumber \\
&=&\frac{a^2\theta_0^2}{L}\{icos(\alpha+\theta_0)-sin(\alpha+\theta_0)\}-\frac{a^2\theta_0^2}{L}\alpha\{cos(\alpha+\theta_0)+isin(\alpha+\theta_0)\} \nonumber \\
\end{eqnarray}
となる。これを$\;x,y\;$座標で表すと次のようになる。
\begin{eqnarray}
G'_x&=&-\frac{a^2\theta_0^2}{L}\{sin(\alpha+\theta_0)+\alpha cos(\alpha+\theta_0)\} \\
G'_y&=&\frac{a^2\theta_0^2}{L}\{cos(\alpha+\theta_0)-\alpha sin(\alpha+\theta_0)\}
\end{eqnarray}
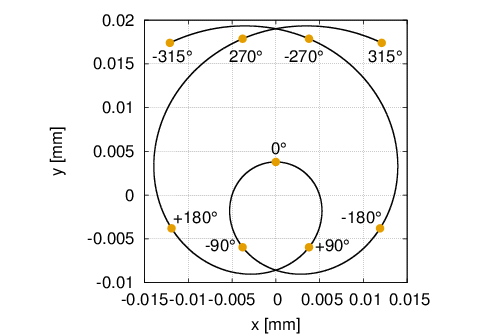
これを図示すると上図のようになる。図では重心点が静止時にも原点を通過しない。図は内端取付点から
自由外端までのヒゲ全体の重心点の軌跡であるが、ヒゲゼンマイの形状は原点に対し偏心なく取り付けられているものとする。
取り付け点より内側、アルキメデス曲線の位置を表す角度$\;\theta\;$で言えば$\;(0,\theta_0)\;$の区間、
つまりヒゲ玉の中に仮想する原点からヒゲ取付点までの回転角$\;\theta_0\;$のアルキメデス曲線の重心が
ヒゲ全体から欠落しているのであるからヒゲゼンマイの重心点は静止点で座標中心、つまり天真に一致しない。
次にこのようなヒゲゼンマイの重心点移動がどのようなトルクとなるかまた等時性誤差への影響を計算する。
ヒゲの重心点による天真まわりのトルクは$\;g\;$を重力加速度としてヒゲ質量$\;m\;$と重心点の$\;x\;$座標$\;G'_x\;$の積$\;mgG'_x\;$
であるからテンワの運動方程式はテンワの慣性モーメント$\;I\;$,ヒゲゼンマイのバネ定数$\;k\;$として
\begin{eqnarray}
I\frac{d^2\theta}{dt^2}=-mgG'_x-k\theta
\end{eqnarray}
となる。これに式(4)を代入して整理すると
\begin{eqnarray}
I\frac{d^2\theta}{dt^2}+k\theta=mg\frac{a^2\theta_0^2}{L}\{sin(\alpha+\theta_0)+\alpha cos(\alpha+\theta_0)\}
\end{eqnarray}
となる。
3-1から外乱$\;f(\theta)\;$があるときの等時性誤差は
\begin{eqnarray}
\delta=-\frac{1}{A^2kT}\int_0^T\theta f(\theta) dt
\end{eqnarray}
と表される。今回は外乱トルク$\;f(\theta)\;$が式(7)の右辺であるから
式(8)にこれを代入して三角関数の加法定理(第5部 数学公式集 5-1-4)を使えば
\begin{eqnarray}
\delta&=&-\frac{1}{A^2Tk}\int_0^T\alpha f(\alpha)dt \nonumber \\
&=&-\frac{mga^2\theta_0^2}{A^2TkL}\int_0^T\alpha \{sin(\alpha+\theta_0)+\alpha cos(\alpha+\theta_0)\} dt \nonumber \\
&=&-\frac{mga^2\theta_0^2}{A^2TkL}\int_0^T\{\alpha sin(\alpha+\theta_0)+\alpha^2cos(\alpha+\theta_0)\}dt \nonumber \\
&=&-\frac{mga^2\theta_0^2}{A^2TkL}\int_0^T(\alpha sin\alpha cos\theta_0+\alpha cos\alpha sin\theta_0+\alpha^2cos\alpha cos\theta_0-\alpha^2sin\alpha sin\theta_0)dt \nonumber \\
\end{eqnarray}
ここで第5部 数学公式集 5-5及び3-4-3から
\begin{eqnarray}
\int_0^T\alpha^2cos\alpha dt&=&TA\{AJ_0(A)-J_1(A)\} \\
\int_0^T\alpha^2sin\alpha dt&=&0 \\
\int_0^T\alpha cos\alpha dt&=&0 \\
\int_0^T\alpha sin\alpha dt &=&ATJ_1(A)
\end{eqnarray}
であるから
\begin{eqnarray}
\delta&=&-\frac{mga^2\theta_0^2}{A^2TkL}\{cos\theta_0ATJ_1(A)+cos\theta_0AT[AJ_0(A)-J_1(A)]\} \nonumber \\
&=&-\frac{mga^2\theta_0^2}{kL}cos\theta_0J_0(A) \nonumber \\
&=&-(\frac{T}{2\pi})^2\frac{mg}{I}\frac{a^2\theta_0^2}{L}cos\theta_0J_0(A)
\end{eqnarray}
またヒゲの長さ$\;L\;$は概略$\;L=a\theta_1^2/2\;$であり、ヒゲの外端半径$\;R\;$、内端半径$\;R_0\;$を使えば
$\;R=a\theta_1,R_0=a\theta_0\;$であるからこれを式(13)に代入すると
\begin{eqnarray}
\delta=-\chi (\frac{T}{2\pi})^2\frac{mg}{I}2a(\frac{R_0}{R})^2cos\theta_0J_0(A)
\end{eqnarray}
となる。ここで$\;\chi\;$はヒゲの外端は固定されており質量$\;m\;$は実質的には内端部分の質量しか効いてこない実状に
合わせるための補正係数で小牧氏の論文によればこれを$0.5$としている。式(14)からヒゲ重心移動の大きさは
内端半径と外径の比の2乗に比例する。またヒゲのピッチに比例、すなわち巻数に反比例することがわかる。
また式(14)には$\;cos\theta_0\;$が含まれているので原点から内端点までの仮想アルキメデス曲線の回転角度が
$\;n\pi \pm \pi/2\;$のときヒゲの重心移動による等時性誤差は0になる。
下図に$\;J_0(A)cos\theta_0\;$の値を示す。これよりヒゲゼンマイの重心移動による等時性誤差は振り角が
138°(正確には137.7863549°)のとき0となり220°(正確には219.5405804°)のとき最大となる。
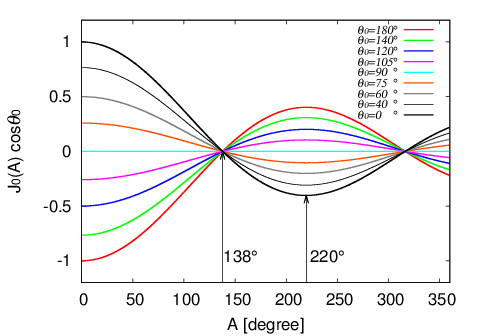
振り角220°で姿勢差を見るとテンワの片重りの影響が出ないため、ヒゲの重心を調整する上では都合が良い。
等時性誤差には他にもヒゲの偏心や脱進機誤差、天真ほぞの振れなどが含まれるため実際にはヒゲの重心移動による
影響だけを分離して見ることは出来ないが、振り角220°の姿勢差を見ることによってどこまで正しいヒゲの重心に
近づけられたかを見極めるといった見方が現実的である。
ここで例として
ヒゲの外端半径$\;R=2.5mm=0.0025\;[m]\;$,ヒゲの内径$\;R_0=0.7mm=0.0007[m]\;$,ヒゲのピッチ$\;p=0.14mm\;$
すなわち$\;a=p/2\pi=0.02228mm=0.00002228\;[m]\;$周期$\;T=0.333\;[s]\;$(6振動),ヒゲの質量$\;m=5mg=5\times10^{-6}\;[kg]\;$,
テンプの慣性モーメント$\;I=1.4\times10^{-9}\;[kgm^2]\;$とし、これらを式(14)に代入しこれを86400倍して日差に換算すると
ヒゲの重心移動による等時性誤差は下図のようになる。

ヒゲの重心移動量そのものはヒゲ内端形状でほぼ決まるのため、これによる等時性誤差はあまり小さくは出来ないと
考えた方が良い。
ただしフィリップスの条件を満たす内端曲線を持つ場合はヒゲの重心移動による等時性誤差は理論上0である。



