平ヒゲの等時性誤差は3-3-6で求めた
\begin{eqnarray}
\delta=\frac{1}{2A^2TI_h}\int_0^T\alpha \frac{d|\Delta|^2}{d\alpha}dt
\end{eqnarray}
を計算すればよい。アルキメデス曲線のヒゲについて$\;\Delta\;$が3-4-2から
\begin{eqnarray}
\Delta=\frac{a^2}{L}\alpha[\theta_1^2exp\{i\theta_1\}-\theta_0^2exp\{i(\alpha+\theta_0)\}]
\end{eqnarray}
のように得られたからこれを式(1)に入れる。$\;\Delta\;$の実数部$\;\Delta_x\;$と虚数部$\;\Delta_y\;$とは式(2)から直ちに
\begin{eqnarray}
\Delta_x=\frac{\alpha}{L}a^2[\theta_1^2cos\theta_1-\theta_0^2cos(\theta_0+\alpha)] \nonumber \\
\Delta_y=\frac{\alpha}{L}a^2[\theta_1^2sin\theta_1-\theta_0^2sin(\theta_0+\alpha)] \nonumber
\end{eqnarray}
のように得られる。
この自乗和を作ると三角関数の加法定理(第5部 数学公式集 5-1-4)より
\begin{eqnarray}
|\Delta|^2=\frac{\alpha^2}{L^2}a^4[\theta_1^4+\theta_0^4-2\theta_1^2\theta_0^2cos(\alpha+\theta_0-\theta_1)]
\end{eqnarray}
となるからこれを$\;\alpha\;$で微分して
\begin{eqnarray}
\frac{d|\Delta|^2}{d\alpha}&=&\frac{2\alpha}{L^2}a^4[\theta_1^4+\theta_0^4-2\theta_1^2\theta_0^2\;cos(\alpha+\theta_0-\theta_1)] \nonumber \\
&\;&+\frac{2}{L^2}\alpha^2a^4\theta_1^2\theta_0^2\;sin(\alpha+\theta_0-\theta_1)
\end{eqnarray}
を得る。これを式(1)に入れると等時性誤差$\;\delta\;$が
\begin{eqnarray}
\delta&=&\frac{a^4}{TA^2I_hL^2}\int_0^T[\alpha^2\{\theta_1^4+\theta_0^4-2\theta_1^2\theta_0^2\;cos(\alpha+\theta_0-\theta_1)\} \nonumber \\
&\;&+\alpha^3\theta_1^2\theta_0^2\;sin(\alpha+\theta_0-\theta_1)]dt \nonumber
\end{eqnarray}
のように表される。$\;L\;$と$\;I_h\;$とに3-4-1で求めた
\begin{eqnarray}
L=\frac{a}{2}(\theta_1^2-\theta_0^2) \\
I_h=\frac{a^2}{4}(\theta_1^2+\theta_0^2)
\end{eqnarray}
を入れ、三角関数の加法定理(第5部 数学公式集 5-1-4)を使えば
\begin{eqnarray}
\delta&=&\frac{16}{TA^2(\theta_1^2+\theta_0^2)(\theta_1^2-\theta_0^2)^2}[(\theta_1^4+\theta_0^4)\int_0^T\alpha^2dt \nonumber \\
&\;&-2\theta_1^2\theta_0^2\int_0^T\alpha^2cos(\alpha+\theta_0-\theta_1)dt \nonumber \\
&\;&+\theta_1^2\theta_0^2\int_0^T\alpha^3sin(\alpha+\theta_0-\theta_1)dt] \nonumber \\
&=&\frac{16}{TA^2(\theta_1^2+\theta_0^2)(\theta_1^2-\theta_0^2)^2}[(\theta_1^4+\theta_0^4)\int_0^T\alpha^2dt \nonumber \\
&\;&-2\theta_1^2\theta_0^2\int_0^T\alpha^2\{cos \alpha\;cos(\theta_1-\theta_0)+sin \alpha\;sin (\theta_1-\theta_0)\}dt \nonumber \\
&\;&+\theta_1^2\theta_0^2\int_0^T\alpha^3\{sin\alpha \;cos(\theta_1-\theta_0)-cos\alpha \;sin(\theta_1-\theta_0)\}dt]
\end{eqnarray}
のようになる。この式の$\alpha$に3-1の式(6)から
\begin{eqnarray}
\alpha=A\;sin\omega t
\end{eqnarray}
を入れて積分するのであるが、そうすると三角関数の中に三角関数の入ったものの積分になる。それにはベッセル関数を用いて
\begin{eqnarray}
cos(Asin\;t)&=&J_0(A)+2J_2(A)cos2t+2J_4(A)cos4t+\cdots \\
sin(Asin\;t)&=&2J_1(A)sin\;t+2J_3(A)sin3t+2J_5(A)sin5t\cdots
\end{eqnarray}
なる展開公式を使用する(第5部 数学公式集 5-5)。そうすると
\begin{eqnarray}
\int_0^T\alpha^2dt&=&A^2\int_0^{2\pi/\omega}sin^2\omega t dt=A^2\frac{\pi}{\omega}=\frac{1}{2}A^2T \\
\int_0^T\alpha^2cos\alpha dt&=&A\int_0^Tsin^2\omega t\;cos(Asin\omega t)dt \nonumber \\
&=&\frac{A^2}{2}\int_0^T(1-cos2\omega t)\{J_0+2J_2cos2\omega t+2J_4cos4\omega t+\cdots\}dt \nonumber \\
&=&\frac{A^2}{2}\{J_0T-J_2T\} \nonumber
\end{eqnarray}
これに
\begin{eqnarray}
J_2(A)=\frac{2}{A}J_1(A)-J_0(A) \nonumber
\end{eqnarray}
を入れて結局
\begin{eqnarray}
\int_0^T\alpha^2cos\alpha dt=TA\{AJ_0(A)-J_1(A)\}
\end{eqnarray}
を得る。更に
\begin{eqnarray}
\int_0^T\alpha^2sin\alpha dt&=&\frac{A^2}{2}\int_0^T(1-cos2\omega t)\{2J_1sin\omega t+2J_3sin3\omega t+\cdots\}dt \nonumber \\
=0 \\
\int_0^T\alpha^3cos\alpha dt &=&0 \\
\int_0^T\alpha^3sin\alpha dt&=&\frac{A^3}{4}\int_0^T(3sin\omega t-sin3\omega t)\{2J_1sin\omega t \nonumber \\
&\;&+2J_3sin3\omega t+2J_5sin5\omega t+\cdots\}dt \nonumber \\
&=&\frac{A^3}{4}\{3J_1T-J_3T\} \nonumber
\end{eqnarray}
これに
\begin{eqnarray}
J_3(A)=\frac{4}{A}J_2-J_1=(\frac{8}{A^2}-1)J_1-J_0 \nonumber
\end{eqnarray}
を入れ
\begin{eqnarray}
\int_0^T\alpha^3sin\alpha dt=TA\{(A^2-2)J_1(A)+AJ_0(A)\}
\end{eqnarray}
を得る。これらの関係を使えば式(7)の積分ができて
\begin{eqnarray}
\delta&=&\frac{16}{A^2T(\theta_1^2+\theta_0^2)(\theta_1^2-\theta_0^2)^2}[(\theta_1^4+\theta_0^4)\frac{A^2T}{2}
-2\theta_1^2\theta_0^2cos(\theta_1-\theta_0)TA\{AJ_0-J_1\} \nonumber \\
&\;&+\theta_1^2\theta_0^2cos(\theta_1-\theta_0)TA\{(A^2-2)J_1+AJ_0\}] \nonumber \\
&=&\frac{8(\theta_1^4+\theta_0^4)}{(\theta_1^2+\theta_0^2)(\theta_1^2-\theta_0^2)^2} \nonumber \\
&\;&+\frac{16\theta_1^2\theta_0^2}{(\theta_1^2+\theta_0^2)(\theta_1^2-\theta_0^2)^2}
cos(\theta_1-\theta_0)\{AJ_1(A)-J_0(A)\}
\end{eqnarray}
が得られる。これが求める等時性誤差の式である。この式の第1項は振り角$\;A\;$を含まないから近似公式を使った
周期に対する補正値を表すだけである。第2項は振り角$\;A\;$の関数で、振り角によって周期が変わることを表している。
一例として3-4-1で用いた数値
$\theta_0=8\pi,\;\;\;\;\;\theta_1=33\pi$
を入れると式(16)は
\begin{eqnarray}
\delta=[8+cos(\theta_1-\theta_0)\{AJ_1-J_0\}]\times 10^{-4}
\end{eqnarray}
となる。この式の中で$\;\phi=(\theta_1-\theta_0)\;$とおいて振り角を含む項$\;\{AJ_1(A)-J_0(A)\}\;$を振り角の関数として図示すると図のようになる。

図からわかるように振り角が234°のときこの関数値は0になる。したがってこの場合の等時性誤差は
式(17)の右辺第1項のみの進み歩度となる。また振り角が157°のとき等時性誤差は最大値となることがわかる。
また$\;\phi=90^\circ\;$(または$\;270^\circ\;$)のとき$\;cos\phi=0\;$となるから等時性誤差は最も小さくなる。
これは特にカスパリ効果と呼ばれる。
一方$\;\phi=0^\circ\;$及び$\;\phi=180^\circ\;$のときは振り角の影響が最も大きくなって等時性誤差が大きくなる。
ただしこれらはヒゲの形が正しいアルキメデス曲線をもつ場合にのみ成り立つものである。
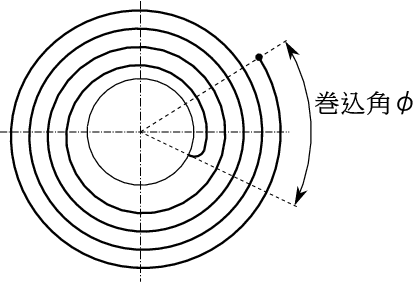
$\;\phi\;$はヒゲの巻き始めの位置から測った巻き終わりまでの角度で$\;30\pi\;$近い大きな値であるが、
その$\;cos\;$が問題なのであるから$\;2\pi\;$の整数倍を落としてその端数だけに着目すればよい。
これは図に示すように天真の中心から見てヒゲの内端の方向と外端の方向とのなす角でこの角度を巻込角と呼んでいる。
平ヒゲはその形状が与えられると式(17)の右辺第1項で計算される振り角によらない固定の進み歩度が与えられ、
更に第2項の振り角に依存した等時性誤差が発生する。ここで実際のヒゲの調整では巻込角を$\;\pm 90^\circ\;$の範囲で
変化させながら進みの度合いを調節し脱進機誤差の遅れと相殺させて精度を高めるという工夫をしている。
式(17)の第1項は等時性誤差には影響しないので、これを省略し巻込角$\;\phi\;$による振り角に依存する
等時性誤差を簡略化して求めておいた方が実用的である。
式(17)の右辺第1項を省略し、$\;\theta_0=r_0/a,\theta_1=r_1/a,L=\frac{a}{2}(\theta_1^2-\theta_0^2),\phi=\theta_1-\theta_0\;$とおくと式(17)は
\begin{eqnarray}
\frac{4r_1^2r_0^2}{(r_1^2+r_0^2)L^2}cos\phi \{AJ_1(A)-J_0(A)\}
\end{eqnarray}
ここで$\;r_1\gg r_0\;$であるから
\begin{eqnarray}
\delta=\frac{4r_0^2}{L^2}cos\phi \{AJ_1(A)-J_0(A)\}
\end{eqnarray}
と覚えやすい形に簡略化される。
これが最も実用的な巻込角の等時性誤差に対する影響を表す式である。
尚、実際の腕時計では巻込角$\;\phi\;$の値を巻込角$\;\phi+\alpha\;$として手計算した方が現実にあっているようである。
$\;\alpha\;$の値は小牧氏の論文によれば15°くらいと推定されている。